|
|
|
|
|
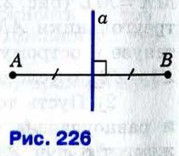
§ 3. Четыре замечательные точки треугольника Свойства серединного перпендикуляра к отрезкуСерединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему. На рисунке 226 прямая а — серединный перпендикуляр к отрезку АВ.
Докажем теорему о серединном перпендикуляре к отрезку. Теорема
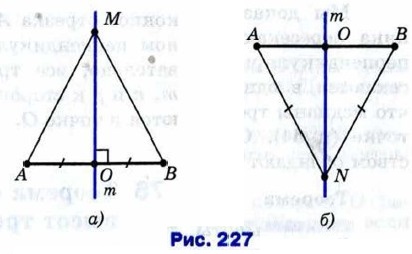
Доказательство Пусть прямая m — серединный перпендикуляр к отрезку АВ, точка О — середина этого отрезка (рис. 227, а). 1) Рассмотрим произвольную точку М прямой m и докажем, что AM = ВМ. Если точка M совпадает с точкой О, то это равенство верно, так как О — середина отрезка АВ. Пусть M и О различные точки. Прямоугольные треугольники ОAM и ОВМ равны по двум катетам (ОА = ОВ, ОМ — общий катет), поэтому AM = ВМ.
|
|
|