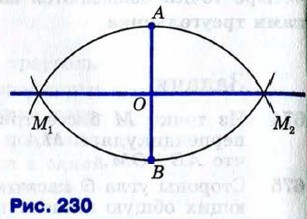
Задачи к § 3. Четыре замечательные точки треугольника (окончание)

686. Постройте серединный перпендикуляр к данному отрезку.

Решение

Пусть АВ — данный отрезок. Построим две окружности с центрами в точках А и В радиуса АВ (рис. 230). Эти окружности пересекаются в двух точках М₁ и М₂. Отрезки АМ₁, AM₂, ВМ₁, ВМ₂ равны друг другу как радиусы этих окружностей.

Проведём прямую М₁М₂. Она является искомым серединным перпендикуляром к отрезку АВ. В самом деле, точки М₁ и М₂ равноудалены от концов отрезка АВ, поэтому они лежат на серединном перпендикуляре к этому отрезку. Значит, прямая М₁М₂ и есть серединный перпендикуляр к отрезку АВ.

687. Даны прямая а и две точки А и В, лежащие по одну сторону от этой прямой. На прямой а постройте точку М, равноудалённую от точек А к В.

688. Даны угол и отрезок. Постройте точку, лежащую внутри данного угла, равноудалённую от его сторон и равноудалённую от концов данного отрезка.

Ответы к задачам § 3. Четыре замечательные точки треугольника

674. Указание. Сначала доказать, что треугольник АОВ равнобедренный.

676. а) 10 см; б) 7√2 дм.

678. а) 46° и 46°; б) 21° и 21°.

679. a) АВ = 3,5 см, CD= 5 см; б) АС = 14,6 см.

681. 9 см.

683. Указание. Воспользоваться методом доказательства от противного.

687. Указание. Воспользоваться теоремой п. 75.

688. Указание. Учесть, что искомая точка лежит на биссектрисе данного угла.

<<< К началу