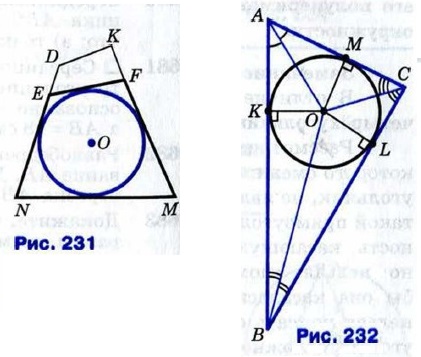
Вписанная окружность

Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности. На рисунке 231 четырёхугольник EFMN описан около окружности с центром О, а четырёхугольник DKMN не является описанным около этой окружности, так как сторона DK не касается окружности. На рисунке 232 треугольник АВС описан около окружности с центром О.

Докажем теорему об окружности, вписанной в треугольник.

Теорема

В любой треугольник можно вписать окружность.

Доказательство

Рассмотрим произвольный треугольник АВС и обозначим буквой О точку пересечения его биссектрис. Проведём из точки О перпендикуляры OK, OL и ОМ соответственно к сторонам АВ, ВС и СА (см. рис. 232). Так как точка О равноудалена от сторон треугольника АВС, то OK = OL = ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны треугольника АВС касаются этой окружности в точках К, L, М, так как они перпендикулярны к радиусам OK, OL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС. Теорема доказана.

Замечание 1

Отметим, что в треугольник можно вписать только одну окружность.

В самом деле, допустим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудалён от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают.

Окончание >>>