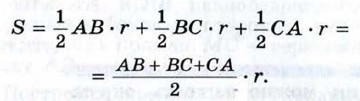|
|
|
|
|
§ 4. Вписанная и описанная окружности Вписанная окружность (окончание)Замечание 2 Обратимся к рисунку 232. Мы видим, что треугольник АВС составлен из трёх треугольников: ABO, ВСО и САО. Если в каждом из этих треугольников принять за основание сторону треугольника АВС, то высотой окажется радиус r окружности, вписанной в треугольник АВС. Поэтому площадь S треугольника АВС выражается формулой
Таким образом,
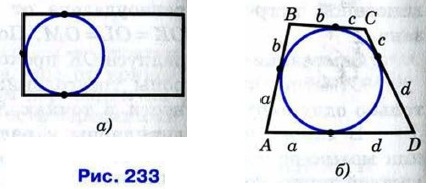
Замечание 3 В отличие от треугольника не во всякий четырёхугольник можно вписать окружность. Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т. е. прямоугольник, не являющийся квадратом. Ясно, что в такой прямоугольник можно «поместить» окружность, касающуюся трёх его сторон (рис. 233, а), но нельзя «поместить» окружность так, чтобы она касалась всех четырёх его сторон, т. е. нельзя вписать окружность. Если же в четырёхугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
Это свойство легко установить, используя рисунок 233, б, на котором одними и теми же буквами обозначены равные отрезки касательных. В самом деле, АВ + CD = а + b + с + d, ВС + AD-a + b + c + d, поэтому АВ + CD = ВС + AD. Оказывается, верно и обратное утверждение:
|
|
|