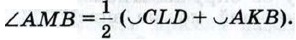|
|
|
|
|
Глава VIII Окружность Дополнительные задачи к главе VIII712. Докажите, что касательные, проведённые через концы хорды, не являющейся диаметром окружности, пересекаются. 713. Прямые АВ и АС — касательные к окружности с центром О, В и С — точки касания. Через произвольную точку X, взятую на дуге ВС, проведена касательная к этой окружности, пересекающая отрезки АВ и АС в точках М и N. Докажите, что периметр треугольника AMN и величина угла MON не зависят от выбора точки X на дуге ВС. 714.* Две окружности имеют общую точку М и общую касательную в этой точке. Прямая АВ касается одной окружности в точке А, а другой — в точке В. Докажите, что точка М лежит на окружности с диаметром АВ. 715. Диаметр АА1 окружности перпендикулярен к хорде ВВи Докажите, что градусные меры дуг АВ и АВ1 меньших полуокружности, равны. 716. Точки А, В, С и D лежат на окружности. Докажите, что если 717. Отрезок АВ является диаметром окружности, а хорды ВС и AD параллельны. Докажите, что хорда CD является диаметром. 718. По данным рисунка 237 докажите, что
Решение Проведём хорду ВС. Так как ∠AMB — внешний угол треугольника ВМС, то ∠AMB = ∠1 + ∠2. По теореме о вписанном угле 719. Через точку, лежащую вне окружности, проведены две секущие. Докажите, что угол между ними измеряется полуразностью дуг, заключённых внутри угла. 720. Может ли вершина разностороннего треугольника лежать на серединном перпендикуляре к какой-либо стороне? Ответ обоснуйте. 721. Докажите, что если в прямоугольник можно вписать окружность, то этот прямоугольник — квадрат. 722. Четырёхугольник ABCD описан около окружности радиуса г. Известно, что АВ : CD = 2 : 3, AD : ВС = 2 : 1. Найдите стороны четырёхугольника, если его площадь равна S. 723. Докажите, что если прямые, содержащие основания трапеции, касаются окружности, то прямая, проходящая через середины боковых сторон трапеции, проходит через центр этой окружности.
|
|
|



 AB =
AB = 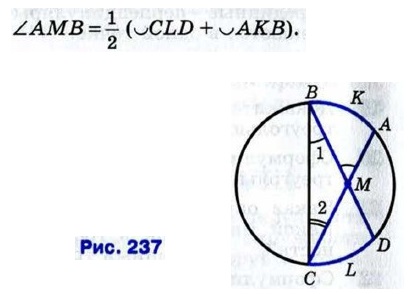
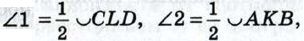 поэтому
поэтому