|
§ 2. Сложение и вычитание векторов



Вычитание векторов
Разностью векторов  и и  называется такой вектор, сумма которого с вектором называется такой вектор, сумма которого с вектором  равна вектору равна вектору 
Разность векторов  и и  обозначается так: обозначается так: 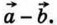
Рассмотрим задачу о построении разности двух векторов.
Задача
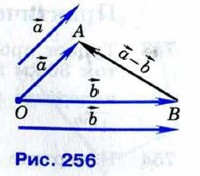
Даны векторы  и и  . Построить вектор . Построить вектор 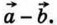
Решение
Отметим на плоскости произвольную точку О и отложим от этой точки векторы 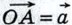 и и 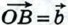 (рис. 256). По правилу треугольника (рис. 256). По правилу треугольника 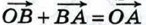 или или  Таким образом, сумма векторов Таким образом, сумма векторов 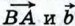 равна равна  . По определению разности векторов это означает, что . По определению разности векторов это означает, что 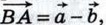 т. е. вектор т. е. вектор  искомый. Задачу о построении разности двух векторов можно решить и другим способом. Прежде чем указать этот способ, введём понятие вектора, противоположного данному. искомый. Задачу о построении разности двух векторов можно решить и другим способом. Прежде чем указать этот способ, введём понятие вектора, противоположного данному.
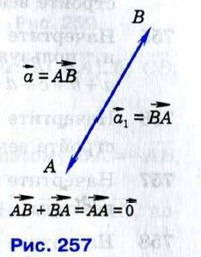
Пусть  — произвольный ненулевой вектор. Вектор — произвольный ненулевой вектор. Вектор  1 называется противоположным вектору 1 называется противоположным вектору  , если векторы , если векторы  и и  1 имеют равные длины и противоположно направлены. На рисунке 257 вектор 1 имеют равные длины и противоположно направлены. На рисунке 257 вектор 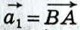 является противоположным вектору является противоположным вектору 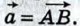 Вектором, противоположным нулевому вектору, считается нулевой вектор. Вектором, противоположным нулевому вектору, считается нулевой вектор.
Вектор, противоположный вектору  , обозначается так: , обозначается так: 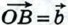 Очевидно, Очевидно, 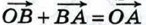
Окончание >>>
| 


 и
и  называется такой вектор, сумма которого с вектором
называется такой вектор, сумма которого с вектором 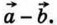
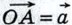 и
и 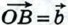 (рис. 256). По правилу треугольника
(рис. 256). По правилу треугольника 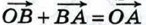 или
или  Таким образом, сумма векторов
Таким образом, сумма векторов 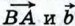 равна
равна 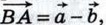 т. е. вектор
т. е. вектор  искомый. Задачу о построении разности двух векторов можно решить и другим способом. Прежде чем указать этот способ, введём понятие вектора, противоположного данному.
искомый. Задачу о построении разности двух векторов можно решить и другим способом. Прежде чем указать этот способ, введём понятие вектора, противоположного данному.
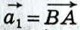 является противоположным вектору
является противоположным вектору 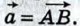 Вектором, противоположным нулевому вектору, считается нулевой вектор.
Вектором, противоположным нулевому вектору, считается нулевой вектор.