|
|
|
|
|
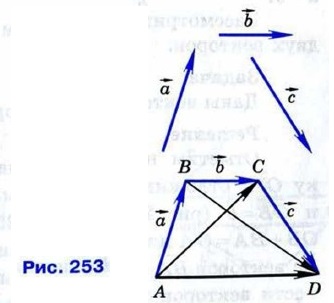
§ 2. Сложение и вычитание векторов Сумма нескольких векторовСложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т. д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. На рисунке 253 показано постро- ение суммы векторов
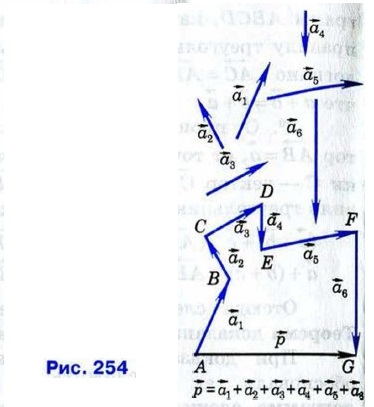
Аналогично можно построить сумму четырёх, пяти и вообще любого числа векторов. На рисунке 254 показано построение суммы шести векторов. Это правило построения суммы нескольких векторов называется правилом многоугольника. Рисунок 254 поясняет название.
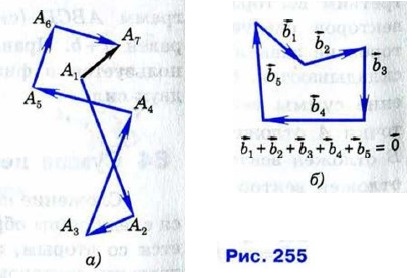
Правило многоугольника можно сформулировать также следующим образом: если А1, А2, ..., Аn — произвольные точки плоскости,
|
|
|



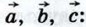 от произвольной точки А отложен вектор
от произвольной точки А отложен вектор 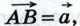 затем от точки B отложен вектор
затем от точки B отложен вектор 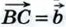 и, наконец, от точки С отложен вектор
и, наконец, от точки С отложен вектор 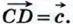 В результате получается вектор
В результате получается вектор 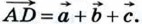
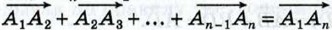 (на рисунке 255, а n = 7). Это равенство справедливо для любых точек А1, А2, ..., Аn, в частности в том случае, когда некоторые из них совпадают. Например, если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору (рис. 255, б).
(на рисунке 255, а n = 7). Это равенство справедливо для любых точек А1, А2, ..., Аn, в частности в том случае, когда некоторые из них совпадают. Например, если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору (рис. 255, б).