|
|
§ 3. Умножение вектора на число. Применение векторов к решению задач



Произведение вектора на число
Прежде чем ввести ещё одно действие — умножение вектора на число, обратимся к примеру. Представим себе, что один автомобиль движется прямолинейно с постоянной скоростью, второй автомобиль движется в том же направлении со скоростью, вдвое большей, а третий автомобиль движется им навстречу, т. е. в противоположном направлении, и величина его скорости такая же, как у второго автомобиля. Если мы изобразим скорость первого автомобиля вектором 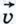 (рис. 260, а), то естественно изобразить скорость второго автомобиля вектором, у которого направление такое же, как у вектора (рис. 260, а), то естественно изобразить скорость второго автомобиля вектором, у которого направление такое же, как у вектора 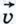 , а длина в два раза больше, и обозначить этот вектор , а длина в два раза больше, и обозначить этот вектор 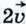 . Скорость третьего автомобиля изобразится вектором, противоположным вектору . Скорость третьего автомобиля изобразится вектором, противоположным вектору 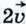 , т. е. вектором , т. е. вектором 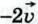 (см. рис. 260, а). Естественно считать, что вектор (см. рис. 260, а). Естественно считать, что вектор 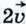 получается умножением вектора получается умножением вектора 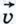 на число 2, а вектор на число 2, а вектор 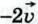 получается умножением вектора получается умножением вектора 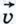 на число -2. Этот пример подсказывает, каким образом следует ввести умножение вектора на число. на число -2. Этот пример подсказывает, каким образом следует ввести умножение вектора на число.

Произведением ненулевого вектора  на число k называется такой вектор на число k называется такой вектор  , длина которого равна , длина которого равна 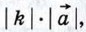 причём векторы причём векторы  и и  сонаправлены при k ≥ 0 и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор. сонаправлены при k ≥ 0 и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение вектора  на число k обозначается так: на число k обозначается так: 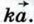 На рисунке 260, б изображены вектор На рисунке 260, б изображены вектор  и векторы и векторы 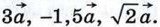
Из определения произведения вектора на число непосредственно следует, что:
1) произведение любого вектора на число нуль есть нулевой вектор;
2) для любого числа k и любого вектора  векторы векторы  и и 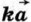 коллинеарны. коллинеарны.
Окончание >>>
|



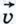 (рис. 260, а), то естественно изобразить скорость второго автомобиля вектором, у которого направление такое же, как у вектора
(рис. 260, а), то естественно изобразить скорость второго автомобиля вектором, у которого направление такое же, как у вектора 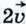 . Скорость третьего автомобиля изобразится вектором, противоположным вектору
. Скорость третьего автомобиля изобразится вектором, противоположным вектору 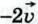 (см. рис. 260, а). Естественно считать, что вектор
(см. рис. 260, а). Естественно считать, что вектор 
 на число k называется такой вектор
на число k называется такой вектор  , длина которого равна
, длина которого равна 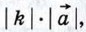 причём векторы
причём векторы 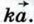 На рисунке 260, б изображены вектор
На рисунке 260, б изображены вектор 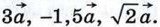
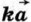 коллинеарны.
коллинеарны.