|
|
|
|
|
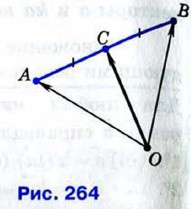
§ 3. Умножение вектора на число. Применение векторов к решению задач Применение векторов к решению задачВекторы могут использоваться для решения геометрических задач и доказательства теорем. Приведём примеры. Рассмотрим сначала вспомогательную задачу. Задача 1 Точка С — середина отрезка АВ, а О — произвольная точка плоскости (рис. 264). Доказать, что
Решение По правилу треугольника
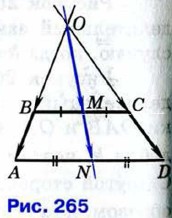
Задача 2 Доказать, что прямая, проведённая через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон. Решение Пусть ABCD — данная трапеция, М и N — середины оснований ВС и AD, а О — точка пересечения прямых АВ и CD (рис. 265). Докажем, что точка О лежит на прямой MN.
Треугольники OAD и ОВС подобны по первому признаку подобия треугольников (докажите это), поэтому Так как
Точка М — середина отрезка ВС, поэтому Подставив в это равенство выражения (1) для
Отсюда следует, что векторы
|
|
|



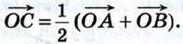
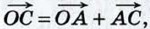
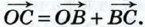 Складывая эти равенства, получаем:
Складывая эти равенства, получаем: 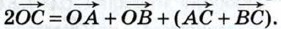 Так как точка С — середина отрезка АВ, то
Так как точка С — середина отрезка АВ, то 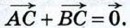 Таким образом,
Таким образом, 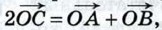 или
или
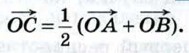
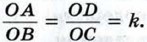
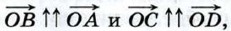 то
то
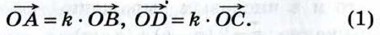
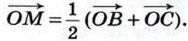 Аналогично
Аналогично 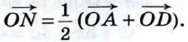
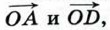 получим:
получим:
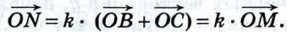
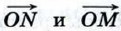 коллинеарны, и, значит, точка О лежит на прямой MN.
коллинеарны, и, значит, точка О лежит на прямой MN.