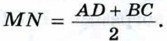|
|
|
|
|
§ 3. Умножение вектора на число. Применение векторов к решению задач Средняя линия трапецииСредней линией трапеции называется отрезок, соединяющий середины её боковых сторон. Докажем теорему о средней линии трапеции. Теорема
Доказательство Пусть MN — средняя линия трапеции ABCD (рис. 266). Докажем, что По правилу многоугольника
Но М и N — середины сторон АВ и CD, поэтому
Так как векторы Теорема доказана.
|
|
|



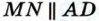 и
и 
 и
и 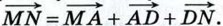 Сложив эти равенства, получим:
Сложив эти равенства, получим:
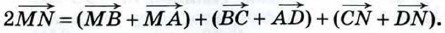
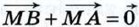 и
и  Следовательно,
Следовательно, 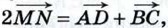 откуда
откуда
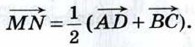
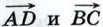 сонаправлены, то векторы
сонаправлены, то векторы 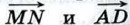 также сонаправлены, а длина вектора
также сонаправлены, а длина вектора 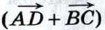 равна AD + BC. Отсюда следует, что
равна AD + BC. Отсюда следует, что 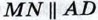 и
и