|
|
|
|
|
Глава VII. Подобные треугольники Задачи повышенной трудности к главе VII. Подобные треугольники847. На рисунке 269 изображён правильный пятиугольник ABCDE, т. е. выпуклый пятиугольник, у которого все углы равны и все стороны равны. Докажите, что:
848. В треугольнике АВС (АВ * АС) через середину М стороны ВС проведена прямая, Рис. 269 параллельная биссектрисе угла А, которая пересекает прямые АВ и АС соответственно в точках D и Е. Докажите, что BD = CE. 849. Докажите, что отрезки, соединяющие основания высот остроугольного треугольника, образуют треугольник, в котором эти высоты являются биссектрисами. 850. Точки Е и F лежат на стороне АВ треугольника АВС, причём точка Е лежит на отрезке AF и AE = BF. Прямая, проведённая через точку Е параллельно стороне АС, пересекает прямую, проведённую через точку F параллельно стороне ВС, в точке К. Докажите, что точка К лежит на медиане треугольника АВС, проведённой к стороне АВ. 851. Гипотенуза прямоугольного треугольника является стороной квадрата, не перекрывающегося с этим треугольником. Найдите расстояние от точки пересечения диагоналей квадрата до вершины прямого угла треугольника, если сумма катетов равна а. 852. В треугольнике 853. Из точки М внутренней области угла АОВ проведены перпендикуляры МР и MQ к его сторонам О А и ОБ. Из точек Р и Q проведены перпендикуляры PR и QS соответственно к ОБ и О А. Докажите, что RS ⊥ ОМ. 854. В равнобедренном треугольнике АВС из середины D основания АС проведён перпендикуляр DH к стороне ВС. Пусть М — середина отрезка DH. Докажите, что ВМ ⊥АН. 855. Из вершины прямого угла С прямоугольного треугольника АВС проведён перпендикуляр CD к гипотенузе, а из точки D — перпендикуляры DE и DF к катетам АС и ВС. Докажите, что:
856. Диагонали выпуклого четырёхугольника ABCD пересекаются в точке Р. Известно, что 857. Точка М не лежит на прямых, содержащих стороны параллелограмма ABCD. Докажите, что существуют точки N, Р и Q, расположенные так, что А, В, С и D являются соответственно серединами отрезков MN, NP, PQ и QM. 858. Докажите, что если противоположные стороны выпуклого четырёхугольника не параллельны, то их полусумма больше отрезка, соединяющего середины двух других противоположных сторон. 859. Докажите, что если сумма расстояний между серединами противоположных сторон выпуклого четырёхугольника равна половине его периметра, то этот четырёхугольник — параллелограмм. 860. Докажите, что если отрезок, соединяющий середины двух противоположных сторон выпуклого четырёхугольника, равен полусумме двух других сторон, то этот четырёхугольник — трапеция или параллелограмм. 861. Диагонали трапеции ABCD пересекаются в точке О. Треугольник АВО, где АВ — меньшее основание трапеции, равносторонний. Докажите, что треугольник, вершинами которого являются середины отрезков ОА, OD и ВС, равносторонний. 862. Из вершины А треугольника АВС проведены перпендикуляры AM и АК к биссектрисам внешних углов этого треугольника при вершинах В и С. Докажите, что отрезок МК равен половине периметра треугольника АВС. 863. Отрезки АА1, ВВ1 и СС1 соединяют вершины треугольника АВС с внутренними точками противоположных сторон. Докажите, что середины этих отрезков не лежат на одной прямой. 864. Середины трёх высот треугольника лежат на одной прямой. Докажите, что этот треугольник прямоугольный. 865. В треугольнике АВС, сторона АС которого в два раза больше стороны ВС, проведены биссектриса СМ и биссектриса внешнего угла при вершине С, пересекающая прямую АВ в точке К. Докажите, что
866. Стороны треугольника EFG соответственно равны медианам треугольника АВС. Докажите, что 867. В треугольнике АВС прямая, проходящая через вершину А и делящая медиану ВМ в отношении 1 : 2, считая от вершины, пересекает сторону ВС в точке К. Найдите отношение площадей треугольников АВК и АВС. 868. Через вершину А параллелограмма ABCD проведена прямая, пересекающая прямые BD, CD и ВС соответственно в точках М, N и Р. Докажите, что отрезок AM является средним пропорциональным между MN и МР. 869. Постройте точку, принадлежащую большему основанию равнобедренной трапеции и отстоящую от данной боковой стороны в га раз дальше, чем от другой (n = 2, 3, 4). 870. Точка С лежит на отрезке АВ. Постройте точку D прямой АВ, не лежащую на отрезке АВ, так, чтобы 871. Постройте равнобедренный треугольник по углу между боковыми сторонами и сумме основания и высоты, проведённой к основанию. 872. Постройте треугольник по двум сторонам и биссектрисе угла между ними. 873. Постройте треугольник АВС, если даны ∠A, ∠C и отрезок, равный сумме стороны АС и высоты ВН. 874. Постройте треугольник по трём высотам. 875. Постройте трапецию по боковой стороне, большему основанию, углу между ними и отношению двух других сторон. 876. Постройте ромб, площадь которого равна площади квадрата, если известно, что отношение диагоналей этого ромба равно отношению данных отрезков.
|
|
|



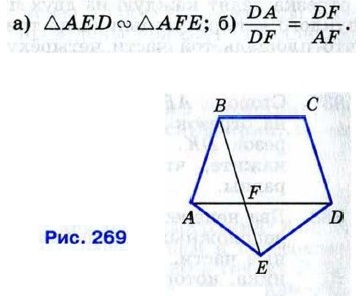
 Докажите, что
Докажите, что 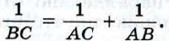
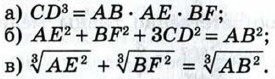
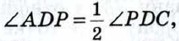
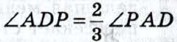 и AD = BD = CD. а) Найдите все углы четырёхугольника, б) Докажите, что АВ2 = ВР • BD.
и AD = BD = CD. а) Найдите все углы четырёхугольника, б) Докажите, что АВ2 = ВР • BD.
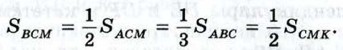
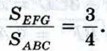
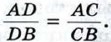 Всегда ли задача имеет решение? DB св
Всегда ли задача имеет решение? DB св