|
|
|
|
|
Глава VI. Площадь Ответы к задачам повышенной трудности: Глава VI. Площадь829. Указание. Воспользоваться равенством треугольников АВС и ADC, АРМ и ATM, MQC и MRC. Для доказательства обратного утверждения предположить, что точка М не лежит на АС, и доказать, что тогда площади параллелограммов не равны. 830. 831. 832. 833. Указание. Пусть АВ — боковая сторона, а М — середина другой боковой стороны трапеции ABCD. Сначала доказать, что 834. 835. Указание. Сначала доказать, что площадь параллелограмма, стороной которого является меньшее основание трапеции, равна сумме площадей двух треугольников, прилежащих к этому основанию и к боковым сторонам трапеции. 836. Указание. Сначала доказать, что SAKM = SCMK и SBKM = SDMK. 837. Указание. Сначала доказать, что SABD = SEDC и SBDK = SCDK. 838. Указание. В каждом из трёх получившихся четырёхугольников провести диагонали так, чтобы никакие две диагонали не имели общего конца, и доказать, что площадь каждого из двух средних треугольников равна полусумме площадей соответствующих крайних треугольников. 839. Указание. Сначала доказать, что SAMB = SADK + SКСВ. 840. 841. 842. Указание. Сначала доказать, что площади треугольников ВТС и ЕТС равны. 843. 844. 845. Указание. Пусть АВ = с, ВС = а, BD = h. Используя теорему Пифагора, доказать, что 846. Указание. Провести перпендикуляры ОМ и ON к сторонам АС и СВ и доказать, что
|
|
|



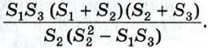 Указание. Воспользоваться следствием 2, п. 53.
Указание. Воспользоваться следствием 2, п. 53.
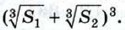 Указание. Воспользоваться второй теоремой п. 53.
Указание. Воспользоваться второй теоремой п. 53.
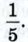
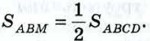
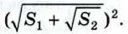 Указание. Сначала доказать, что
Указание. Сначала доказать, что 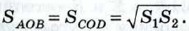
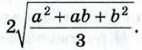 Указание. Пусть АВ и AD — перпендикуляры, проведённые к прямым, содержащим стороны данного угла О, а С — точка пересечения прямых АВ и OD. Рассмотреть прямоугольные треугольники ADC и ОВС.
Указание. Пусть АВ и AD — перпендикуляры, проведённые к прямым, содержащим стороны данного угла О, а С — точка пересечения прямых АВ и OD. Рассмотреть прямоугольные треугольники ADC и ОВС.
 Указание. Учесть, что треугольники ВКС и MCD имеют по равному углу, и воспользоваться второй теоремой п. 53.
Указание. Учесть, что треугольники ВКС и MCD имеют по равному углу, и воспользоваться второй теоремой п. 53.
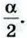 Указание. Сначала доказать, что площади треугольников DC К и DCM равны, а затем доказать, что КМ || DC.
Указание. Сначала доказать, что площади треугольников DC К и DCM равны, а затем доказать, что КМ || DC.
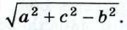 Указание. Через точку М провести прямые, параллельные сторонам прямоугольника, и рассмотреть образовавшиеся прямоугольные треугольники.
Указание. Через точку М провести прямые, параллельные сторонам прямоугольника, и рассмотреть образовавшиеся прямоугольные треугольники.
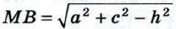 и
и 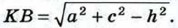
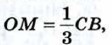
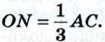 Далее воспользоваться теоремой Пифагора для треугольников АОМ, BON и СОМ.
Далее воспользоваться теоремой Пифагора для треугольников АОМ, BON и СОМ.