|
|
|
|
|
Глава VIII. Окружность Ответы к задачам повышенной трудности: Глава VIII. Окружность877. Указание. Использовать общую касательную к данным окружностям. 878. Указание. Сначала доказать, что AABCojABAD. 879. Указание. Воспользоваться задачей 718. 880. Указание. Рассмотреть два случая: точка пересечения прямых лежит внутри круга и вне круга. В первом случае воспользоваться теоремой о произведении отрезков пересекающихся хорд. 881. Указание. Доказать, что эта величина равна диаметру данной окружности. 882. Указание. Из точек О1 и О2 провести перпендикуляры О1Н1 и О2Н2 к прямой ВС и сравнить расстояние между параллельными прямыми O1H1 и О2Н2 с длиной отрезка О1О2. 883. Пусть CD является диаметром, перпендикулярным к диаметру АВ данной окружности. Искомое множество точек состоит из двух окружностей, построенных на отрезках ОС и OD как на диаметрах. 884. 146° и 107°. Указание. Сначала доказать, что точка М лежит на окружности с центром А радиуса АВ. 885. Указание. Сначала доказать, что проведённые прямые, которые образуют новый треугольник, являются биссектрисами внешних углов треугольника, и воспользоваться теоремой о биссектрисе угла (п. 74). 886. Указание. Для того чтобы доказать, что А' лежит на описанной окружности, сначала надо установить равенство ∠A'CB = ∠BAA'. 887. Указание. Пусть Е — точка пересечения луча BD с окружностью, описанной около треугольника АВС. Воспользоваться подобием треугольников АВЕ и BCD. 888. Указание. Сначала доказать, что ОЕ — серединный перпендикуляр к отрезку АС. 889. Указание. Пусть ХС > ХА и ХС > ХВ. Отложить на отрезке ХС отрезок XD, равный отрезку ХА, учесть, что ∠AXC = 60°, и доказать равенство треугольников АХВ и ADC. 890. Указание. Пусть ABCD — данный четырёхугольник. Провести диаметр ВВ1 и сначала доказать, что AB1 = CD. 891. Указание. Через точку пересечения указанных биссектрис провести прямую, параллельную АВ, до пересечения с прямыми AD и ВС в точках Е и F и доказать, что EF = DC. 892. Указание. Пусть ABCD — данная трапеция, описанная около окружности радиуса r, a AD = a, ВС = b — её основания. Сначала доказать, что 893. Указание. В четырёхугольнике ABCD на диагонали АС взять такую точку К, что ∠ABK = ∠CBD, и далее использовать подобие треугольников АВК и DBC, ВСК и ABD. 894. Указание. Через центр М вписанной окружности провести диаметр PQ описанной окружности и сначала доказать, что РМ • MQ = 2Rr. 895. Указание. Доказать, что точки A1, В1, С1, А2, В2, С2, А3, В3, С3 лежат на окружности с центром в середине отрезка ОН радиуса 896. Указание. Пусть АВС — данный треугольник, а Н, К и М — основания перпендикуляров, проведённых из точки D описанной окружности к прямым АВ, АС и ВС. Допустим, что луч DK лежит внутри угла HDM. Сначала доказать, что ∠AKH = ∠ADH = ∠MDC = ∠MKC. 897. Указание. Пусть О1 и O2 — центры данных окружностей, а r1 и r2 — их радиусы, причём r1 > r2. Построить две окружности с центрами О1 и О2 радиусов соответственно r1 - r2, r1 + r2 и воспользоваться решением задачи 673. 898. Указание. Сначала построить две окружности радиуса P2Q2 с центром М и радиуса ОА с центром О, где А — середина какой-нибудь хорды данной окружности, равной отрезку P1Q1 Затем воспользоваться задачей 897. 899. Указание. Сначала доказать, что наименьшей будет хорда, перпендикулярная к диаметру, проходящему через данную точку. 900. а) Указание. Сначала построить какой-нибудь треугольник по данной стороне и противолежащему углу, затем описать около него окружность и воспользоваться следствием 1, п. 73. б) Указание. Пусть АВС — искомый треугольник, ∠B — данный угол. На продолжении луча АС отложить отрезок АА1 = АВ, а на продолжении луча СА — отрезок СВ1 = ВС. Пользуясь задачей 900, а, сначала построить 901. Указание. Пусть PQR—искомый треугольник, Р — вершина, из которой проведены высота, биссектриса и медиана треугольника, а О — центр описанной около треугольника окружности. Учесть, что 902. Четыре решения. Указание. Воспользоваться задачей 885.
|
|
|



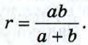
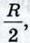 , где R — радиус окружности, описанной около треугольника АВС.
, где R — радиус окружности, описанной около треугольника АВС.
 А1ВВ1.
А1ВВ1.