|
|
§ 1. Координаты вектора



Разложение вектора по двум неколлинеарным векторам (окончание)
1) Вектор 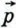 коллинеарен одному из векторов коллинеарен одному из векторов  и и  , например вектору , например вектору 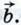 В этом случае по лемме о коллинеарных векторах вектор В этом случае по лемме о коллинеарных векторах вектор 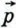 можно представить в виде можно представить в виде 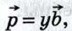 где у — некоторое число, и, следовательно, где у — некоторое число, и, следовательно, 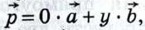 т. е. вектор т. е. вектор 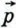 разложен по векторам разложен по векторам  и и  . .
2) Вектор 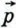 не коллинеарен ни вектору не коллинеарен ни вектору  , ни вектору , ни вектору  . Отметим какую-нибудь точку О и отложим от неё векторы . Отметим какую-нибудь точку О и отложим от неё векторы 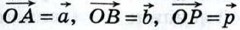 (рис. 274). Через точку Р проведём прямую, параллельную прямой ОВ, и обозначим через A1 точку пересечения этой прямой с прямой О А. По правилу треугольника (рис. 274). Через точку Р проведём прямую, параллельную прямой ОВ, и обозначим через A1 точку пересечения этой прямой с прямой О А. По правилу треугольника 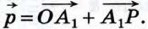 Но векторы Но векторы 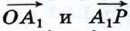 коллинеарны соответственно векторам коллинеарны соответственно векторам  и и  , поэтому существуют такие числа х и у, что , поэтому существуют такие числа х и у, что 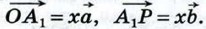 Следовательно, Следовательно, 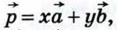 т. е. вектор т. е. вектор  разложен по векторам разложен по векторам  и и  . .
Докажем теперь, что коэффициенты х и у разложения определяются единственным образом. Допустим, что наряду с разложением 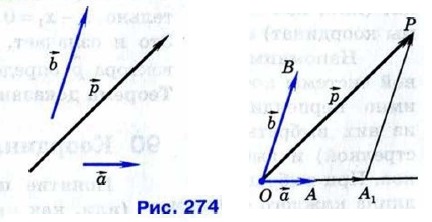 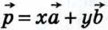 имеет место другое разложение имеет место другое разложение 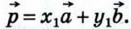 Вычитая второе равенство из первого и используя правила действий над векторами, получаем Вычитая второе равенство из первого и используя правила действий над векторами, получаем 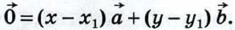 Это равенство может выполняться только в том случае, когда коэффициенты х - х1 и у - у1 равны нулю. В самом деле, если предположить, например, что х - x1 ≠ 0, то из полученного равенства найдём Это равенство может выполняться только в том случае, когда коэффициенты х - х1 и у - у1 равны нулю. В самом деле, если предположить, например, что х - x1 ≠ 0, то из полученного равенства найдём 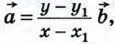 а значит, векторы а значит, векторы  и и  коллинеарны. коллинеарны.
Но это противоречит условию теоремы. Следовательно, х - х1 = 0 и у - у1 = 0, откуда х = х1 и у = у1. Это и означает, что коэффициенты разложения вектора  определяются единственным образом. Теорема доказана. определяются единственным образом. Теорема доказана.
<<< К началу
|



 коллинеарен одному из векторов
коллинеарен одному из векторов  и
и  , например вектору
, например вектору 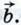 В этом случае по лемме о коллинеарных векторах вектор
В этом случае по лемме о коллинеарных векторах вектор 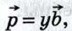 где у — некоторое число, и, следовательно,
где у — некоторое число, и, следовательно, 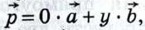 т. е. вектор
т. е. вектор 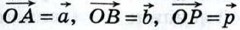 (рис. 274). Через точку Р проведём прямую, параллельную прямой ОВ, и обозначим через A1 точку пересечения этой прямой с прямой О А. По правилу треугольника
(рис. 274). Через точку Р проведём прямую, параллельную прямой ОВ, и обозначим через A1 точку пересечения этой прямой с прямой О А. По правилу треугольника 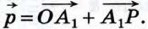 Но векторы
Но векторы 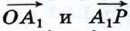 коллинеарны соответственно векторам
коллинеарны соответственно векторам 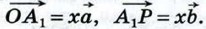 Следовательно,
Следовательно, 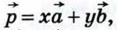 т. е. вектор
т. е. вектор 
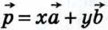 имеет место другое разложение
имеет место другое разложение 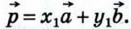 Вычитая второе равенство из первого и используя правила действий над векторами, получаем
Вычитая второе равенство из первого и используя правила действий над векторами, получаем 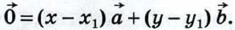 Это равенство может выполняться только в том случае, когда коэффициенты х - х1 и у - у1 равны нулю. В самом деле, если предположить, например, что х - x1 ≠ 0, то из полученного равенства найдём
Это равенство может выполняться только в том случае, когда коэффициенты х - х1 и у - у1 равны нулю. В самом деле, если предположить, например, что х - x1 ≠ 0, то из полученного равенства найдём 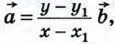 а значит, векторы
а значит, векторы