|
|
|
|
|
§ 1. Координаты вектора Координаты вектораПонятие прямоугольной системы координат (или, как иногда говорят, декартовой системы координат) нам известно из курса алгебры. Напомним, что для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Отложим от начала координат О единичные векторы (т. е. векторы, длины которых равны единице)
Координатные векторы не коллинеарны, поэтому любой вектор Так как нулевой вектор можно представить в виде Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.
|
|
|



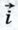 и
и 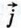 так, чтобы направление вектора
так, чтобы направление вектора 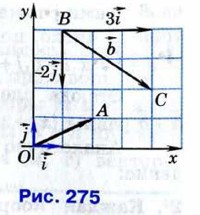
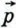 можно разложить по координатным векторам, т. е. представить в виде
можно разложить по координатным векторам, т. е. представить в виде 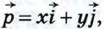 причём коэффициенты разложения (числа х и у) определяются единственным образом. Коэффициенты разложения вектора
причём коэффициенты разложения (числа х и у) определяются единственным образом. Коэффициенты разложения вектора 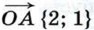 и
и  {3; -2}.
{3; -2}.
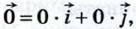 то его координаты равны нулю:
то его координаты равны нулю: 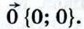 Если векторы
Если векторы 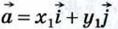 и
и 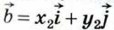 равны, то х1 = х2 и у1 = у2. Таким образом, координаты равных векторов соответственно равны.
равны, то х1 = х2 и у1 = у2. Таким образом, координаты равных векторов соответственно равны.