|
§ 1. Координаты вектора



Координаты вектора (окончание)
Докажем это утверждение для двух векторов. Рассмотрим векторы  {x1; j1} и {x1; j1} и  {х2; у2}. Так как {х2; у2}. Так как 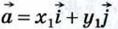 и и 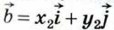 то, пользуясь свойствами сложения векторов и умножения вектора на число, получим: то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:
Отсюда следует, что координаты вектора 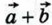 равны {х1 + х2; у1 + у2). равны {х1 + х2; у1 + у2).
Аналогично доказывается следующее утверждение:
| 20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
|
Иными словами, если  {х1; у1) и {х1; у1) и  {х2; у2} — данные векторы, то вектор {х2; у2} — данные векторы, то вектор 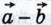 имеет координаты {x1 - х2; y1 - у2). Проведите доказательство самостоятельно. имеет координаты {x1 - х2; y1 - у2). Проведите доказательство самостоятельно.
| 30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
|
В самом деле, пусть вектор  имеет координаты {х; у). Найдём координаты вектора имеет координаты {х; у). Найдём координаты вектора 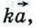 где k — произвольное число. Так как где k — произвольное число. Так как 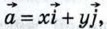 то то 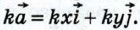 Отсюда следует, что координаты вектора Отсюда следует, что координаты вектора 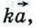 равны {kx; ky}. равны {kx; ky}.
Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами. Пусть, например, требуется найти координаты вектора 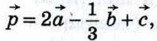 если известно, что если известно, что  {1;-2}, {1;-2},  {0; 3}, {0; 3}, 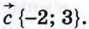
По правилу 30 вектор 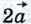 имеет координаты {2; -4}, а вектор имеет координаты {2; -4}, а вектор 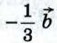 координаты {0; -1}. Так как координаты {0; -1}. Так как 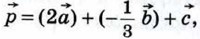 то координаты вектора то координаты вектора 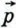 можно найти по правилу 10: {2 + 0 - 2; -4 - 1 + 3}. можно найти по правилу 10: {2 + 0 - 2; -4 - 1 + 3}.
Итак, вектор 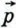 имеет координаты {0; -2}. имеет координаты {0; -2}.
<<< К началу
| 


 {x1; j1} и
{x1; j1} и  {х2; у2}. Так как
{х2; у2}. Так как 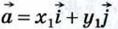 и
и 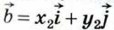 то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:
то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:
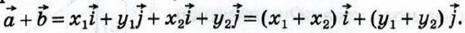
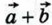 равны {х1 + х2; у1 + у2).
равны {х1 + х2; у1 + у2).
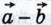 имеет координаты {x1 - х2; y1 - у2). Проведите доказательство самостоятельно.
имеет координаты {x1 - х2; y1 - у2). Проведите доказательство самостоятельно.
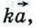 где k — произвольное число. Так как
где k — произвольное число. Так как 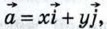 то
то 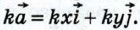 Отсюда следует, что координаты вектора
Отсюда следует, что координаты вектора 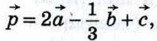 если известно, что
если известно, что 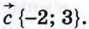
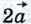 имеет координаты {2; -4}, а вектор
имеет координаты {2; -4}, а вектор 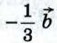 координаты {0; -1}. Так как
координаты {0; -1}. Так как 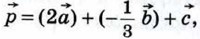 то координаты вектора
то координаты вектора 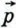 можно найти по правилу 10: {2 + 0 - 2; -4 - 1 + 3}.
можно найти по правилу 10: {2 + 0 - 2; -4 - 1 + 3}.