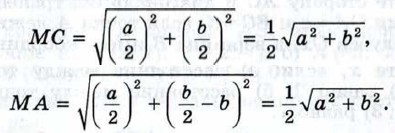|
|
|
|
|
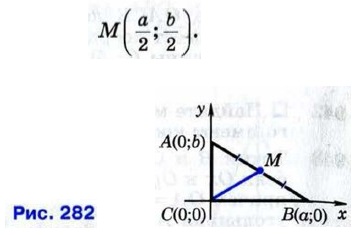
§ 2. Простейшие задачи в координатах Задачи к § 2. Простейшие задачи в координатах (продолжение)Применение метода координат к решению задачФормулы координат середины отрезка и расстояния между двумя точками можно использовать для решения более сложных геометрических задач. С этой целью следует ввести прямоугольную систему координат и записать условие задачи в координатах. После этого решение задачи проводится с помощью алгебраических вычислений. 952. Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин. Решение Рассмотрим прямоугольный треугольник АВС с прямым углом С. Обозначим буквой М середину гипотенузы АВ. Введём прямоугольную систему координат так, как показано на рисунке 282. Если ВС = а, АС = b, то вершины треугольника имеют координаты С (0; 0), В (а; 0), А (0; b). По формулам координат середины отрезка находим координаты точки М:
Пользуясь формулой расстояния между двумя точками, найдём длины отрезков МС и МА:
Таким образом, МА = МВ = МС, что и требовалось доказать. 953. Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей. Решение
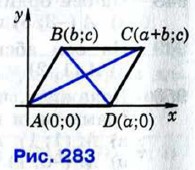
Пусть ABCD — данный параллелограмм. Введём прямоугольную систему координат так, как показано на рисунке 283. Если AD = BC = a, а точка В имеет координаты (b; с), то точка D имеет координаты (а; 0), а точка С — координаты (а + b; с). Используя формулу расстояния между двумя точками, находим: АВ2 = b2 + с2, AD2 = а2, АС2 = (а + b)2 + с2, BD2 = (а - b)2 + с2. Отсюда получаем: АВ2 + ВС2 + CD2 + DA2 = 2 (АВ2 + AD2) = 2 (a2 + b2 + с2), АС2 + BD2 = (а + b)2 + с2 + (а - b)2 + с2 = 2 (а2 + b2 + с2). Таким образом, АВ2 + ВС2 + CD2 + DA2 = АС2 + BD2, что и требовалось доказать. 954. Медиана, проведённая к основанию равнобедренного треугольника, равна 160 см, а основание треугольника равно 80 см. Найдите две другие медианы этого треугольника. 955. Высота треугольника, равная 10 см, делит основание на два отрезка, равные 10 см и 4 см. Найдите медиану, проведённую к меньшей из двух других сторон. 956. Докажите, что в равнобедренной трапеции диагонали равны. Сформулируйте и докажите обратное утверждение. 957. Докажите, что если диагонали параллелограмма равны, то параллелограмм является прямоугольником. 958. Дан прямоугольник ABCD. Докажите, что для произвольной точки М плоскости справедливо равенство AM2 + СМ2 = ВМ2 + DM2.
|
|
|