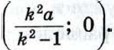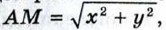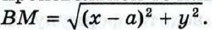|
|
|
|
|
§ 3. Уравнения окружности и прямой Задачи к § 3. Уравнения окружности и прямой (продолжение)Использование уравнений окружности и прямой при решении задач981. Даны две точки А и В. Найдите множество всех точек, для каждой из которых расстояние от точки А в два раза больше расстояния от точки В. Решение Введём прямоугольную систему координат так, как показано на рисунке 289,а. Тогда точки А и В имеют координаты А (0; 0), В (а; 0), где а = АВ.
Найдём расстояния от произвольной точки М (х; у) до точек А и В:
Если точка М (х; у) принадлежит искомому множеству, то AM = 2ВМ, или AM2 = 4ВМ2. Поэтому её координаты удовлетворяют уравнению х2 + у2 = 4 ((х - а)2 + у2). (8) Если же точка М не принадлежит искомому множеству, то её координаты не удовлетворяют этому уравнению. Следовательно, уравнение (8) и есть уравнение искомого множества точек в выбранной системе координат. Раскрывая скобки и группируя слагаемые соответствующим образом, приводим уравнение (8) к виду
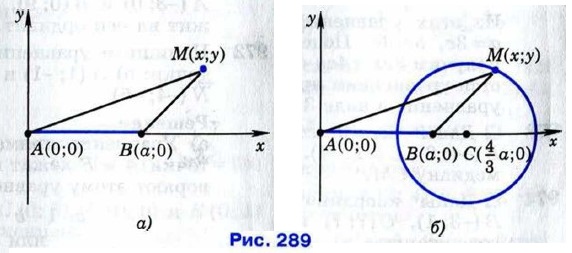
Таким образом, искомым множеством точек является окружность радиуса Замечание Аналогично можно доказать, что множеством всех точек М, удовлетворяющих условию AM = kBM, где k — данное положительное число, не равное единице, является окружность радиуса Эти окружности, соответствующие различным значениям k ≠ 1, называют окружностями Аполлония, поскольку они рассматривались ещё древнегреческим математиком Аполлонием в его трактате «О кругах» во II в. до н. э. Если k = 1, то задача сводится к известной нам задаче о нахождении множества всех точек, равноудалённых от точек А и В. Таким множеством, как мы знаем, является серединный перпендикуляр к отрезку АВ. 982. Точка В — середина отрезка АС, длина которого равна 2. Найдите множество всех точек М, для каждой из которых: a) AM2 + ВМ2 + СМ2 = 50; б) AM2 + 2ВМ2 + 3СМ2 = 4. 983. Даны две точки А и В. Найдите множество всех точек М, для каждой из которых AM2 + ВМ2 = k2, где k — данное число. 984. Даны две точки А и В. Найдите множество всех точек М, для каждой из которых AM2 - ВМ2 = k, где k — данное число. Решение Введём прямоугольную систему координат так, чтобы точка А была началом координат, а точка В имела координаты (а; 0), где а = АВ. Найдём расстояния от произвольной точки М (х; у) до точек А и В: Если точка М (х; у) принадлежит искомому множеству, то AM2 - ВМ2 = k, поэтому координаты точки М удовлетворяют уравнению х2 + у2 - (х - а)2 - у2 = k, или 2ах - а2 - k = 0. Если же точка М не принадлежит искомому множеству, то её координаты не удовлетворяют этому уравнению. Итак, полученное уравнение является уравнением искомого множества точек. Но этим уравнением определяется прямая, параллельная оси Оу, если а2 + k ≠ 0, и сама ось Оу, если a2 + k = 0. Таким образом, искомым множеством точек является прямая, перпендикулярная к прямой АВ. 985. Даны две точки А и B. Найдите множество всех точек М, для каждой из которых ВМ2 - AM2 = 2АВ2. 986. Дан прямоугольник ABCD. Найдите множество всех точек М, для каждой из которых (AM2 + DM2) - (ВМ2 + СМ2) = 2АВ2. 987.* Дан ромб ABCD, диагонали которого равны 2а и 2Ь. Найдите множество всех точек М, для каждой из которых AM2 + DM2 = ВМ2 + СМ2.
|
|
|



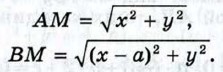
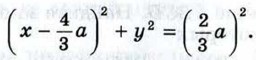
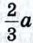 с центром в точке
с центром в точке 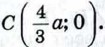 Эта окружность изображена на рисунке 289, б.
Эта окружность изображена на рисунке 289, б.
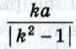 с центром в точке
с центром в точке