|
|
|
|
|
§ 3. Уравнения окружности и прямой Ответы к § 3. Уравнения окружности и прямой960. а) А и С; б) В; в) В и D. 961. а) С; б) В; в) А и D. 963. а) (-4; -3), М;3);б) (4; 3), (-4; 3). 964. а) (3; 0), (3; 10); б) (-2; 5), (8; 5). 965. 1) х2 + у2 = 9; 2) х2 + у2 = 2; 966. а) х2 + (у-5)2 = 9; б) (х + 1)2 + (y - 2)2 = 4; 1 4 967. х2 + у2 = 10. 968. х2 + (у - 6)2 = 25. 969. а) (х - 2)2 + (y - 1)2 = 41; б) (х - 3)2 + (у - 1)2 = 5. 970. (х - 5)2 + у2 = 25, (х + 3)2 + у2 = 25; две окружности. 971. х2 + (у - 4)2 = 25. 972. б) х + у- 7 = 0; в) 3х - 2у + 2 = 0. 973. 7х - у + 3 = 0. 974. а) х - у = 0, у - 1 = 0; б) 3х - 5у + 5 = 0. 975. (-4; 0) и (0; 3). 976. (3;-2). 977. х = 2 и у = 5. 979. 7. 980. 5х + 2у - 10 = 0, 5х - 2у - 10 = 0, 5х + 2у + 10 = 0, 5х - 2у + 10 = 0 или 2х + 5у- 10 = 0, 2х - 5у -10 = 0, 2х + 5y + 10 = 0, 2х - 5у+ 10 = 0. 982. а) Окружность радиуса 4 с центром В; б) окружность радиуса 983. Окружность с центром в точке О радиуса 985. Серединный перпендикуляр к отрезку АВ', где В' и В — точки, симметричные относительно точки А. 986. Прямая ВС. Указание. Выбрать прямоугольную систему координат так, чтобы точки А и В лежали на оси Ох и были симметричны относительно оси Оу. 987. Прямая, проходящая через точку пересечения диагоналей ромба и перпендикулярная к стороне ромба.
|
|
|



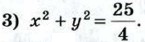
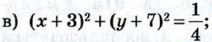 г) (х - 4)2 + (y + 3)2 = 100.
г) (х - 4)2 + (y + 3)2 = 100.
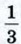 с центром D, лежащим на отрезке ВС, причём
с центром D, лежащим на отрезке ВС, причём 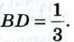
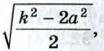 если k2 > 2а2, и точка О, если k2 = 2а2, где О — середина отрезка АВ и
если k2 > 2а2, и точка О, если k2 = 2а2, где О — середина отрезка АВ и 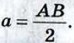 Если k2 < 2а2, то точек, удовлетворяющих условию задачи, не существует.
Если k2 < 2а2, то точек, удовлетворяющих условию задачи, не существует.