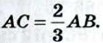|
|
|
|
|
Глава X. Метод координат Ответы на дополнительные задачи к главе X. Метод координат988. 989. а) {-8;-1}, √б5; б) {14; 4}, 2√53; в) {-21; 5}, √466; г) {6;-18}, 6√10. 990. а) {9;-4}, {7;-3}, {1; 21}, {-4; 7}; б) 5, 10, √97, √58. 991. Указание. Ввести вектор 993. Указание. Сначала доказать, что АВ = ВС. 995. (5; 9). 996. а) (-1; 9), (0; 2), (-4; 6); б) 5√2; в) 3√2, 4√2, 5√2. 998. 40. 999. (0; 8) или (-2; 2) или (-8; 0); три решения. 1000. Окружности: а), б), г), д). 1001. (х-3)2 + (y - 5)2 = 25. 1002. 1003. а) 5х - 3у+16 = 0, х + 2у - 6 = 0, 6х - у + 10 = 0; б) 3х + 5у - 4 = 0, 2х - у - 7 = 0, х + 6у - 23 = 0; в) 3х + 5у - 17 = 0, 2х - у + 6 = 0, х + 6у - 10 = 0. 1006. 19,5 см, √261см, 1008. Указание. Систему координат выбрать так, как показано на рисунке 283. 1009. Указание. На продолжении отрезка АА1 отложить отрезок А1А2, равный А А1. Далее воспользоваться задачей 953. 1010. а) Окружность радиуса 2АВ с центром в точке В', симметричной точке В относительно точки А; б) окружность радиуса
|
|
|



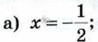 б) не существует; в) х = -2; г) х = 2.
б) не существует; в) х = -2; г) х = 2.
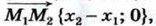 отложить от начала координат вектор
отложить от начала координат вектор 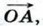 равный
равный 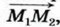 и воспользоваться тем, что абсцисса точки А равна х2 — х1.
и воспользоваться тем, что абсцисса точки А равна х2 — х1.
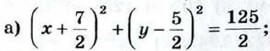 б) (х - 3)2 + (у + 2)2 = 25.
б) (х - 3)2 + (у + 2)2 = 25.
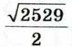 или 12,5 см, √709 см,
или 12,5 см, √709 см, 
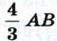 с центром в точке С, лежащей на отрезке АВ, причём
с центром в точке С, лежащей на отрезке АВ, причём