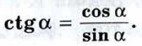|
|
|
|
|
§ 1. Синус, косинус, тангенс, котангенс угла Синус, косинус, тангенс, котангенсВ этой главе получит дальнейшее развитие тригонометрически аппарат геометрии — синус, косинус, тангенс и котангенс будут определены для углов от 0° до 180°. Это даст возможность вывести формулы, связывающие между собой стороны и углы произвольного треугольника. Утверждения об этих формулах называются теоремой синусов и теоремой косинусов. Они широко используются как в самой геометрии, так и в её приложениях, в частности при проведении измерительных работ на местности, Кроме того, в этой главе вводится ещё одно действие над векторами — скалярное умножение векторов. С одной стороны, оно расширяет наши возможности в применении координатно-векторного метода при решении геометрических задач, а с другой — используется в физике для описания физических величин. Введём прямоугольную систему координат Оху и построим полуокружность радиуса 1 с центром в начале координат, расположенную в первом и втором квадрантах (рис. 290). Назовём её единичной полуокружностью. Из точки О проведём луч h, пересекающий единичную полуокружность в точке М (x; у). Обозначим буквой α угол между лучом h и положительной полуосью абсцисс (если луч h совпадает с положительной полуосью абсцисс, то будем считать, что α = 0°).
Если угол а острый, то из прямоугольного треугольника DOM (см. рис. 290) имеем
Но ОМ = 1, MD = у, OD = х, поэтому sin α = у, cos α = х. (1) Итак, синус острого угла α равен ординате у точки М, а косинус угла α — абсциссе х точки М. Если угол α прямой, тупой или развёрнутый (углы АОС, AON и АОВ на рисунке 290) или α = 0°, то синус и косинус угла α также определим по формулам (1). Таким образом, для любого угла а из промежутка 0° ≤ α ≤ 180° синусом угла α называется ордината у точки М, а косинусом угла α — абсцисса х точки М. Так как координаты (x; у) точек единичной полуокружности заключены в промежутках 0≤ у ≤ 1, -1 ≤ x ≤ 1, то для любого α из промежутка 0° ≤ α ≤ 180° справедливы неравенства 0 ≤ sin α ≤ 1, -1 ≤ cos α ≤ 1. Найдём значения синуса и косинуса для углов 0°, 90° и 180°. Для этого рассмотрим лучи О А, ОС и ОВ, соответствующие этим углам (см. рис. 290). Так как точки А, С и В имеют координаты А (1; 0), С (0; 1), В (-1; 0), то sin 0° = 0, sin 90° = 1, sin 180° = 0, (2)
Тангенсом угла α (α ≠ 90°) называется отношение
При α = 90° tg α не определён, поскольку cos 90° = 0, и в формуле (3) знаменатель обращается в нуль. Используя формулы (2), находим: tg 0° = 0, tg 180° = 0. Котангенсом угла α (0° ≤ α ≤ 180°) называется отношение
При α = 0° и α =180° ctg α не определён. Исходя из формул (2), получаем: ctg 90° = 0.
|
|
|



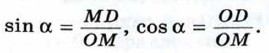
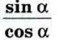 , т. e.
, т. e.

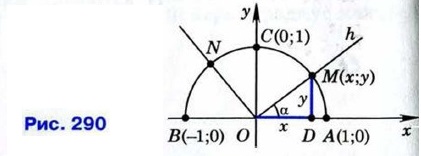
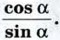 Котангенс угла а обозначает α ется символом ctg α. Таким образом,
Котангенс угла а обозначает α ется символом ctg α. Таким образом,