|
|
|
|
|
§ 1. Синус, косинус, тангенс, котангенс угла Задачи к § 1. Синус, косинус, тангенс, котангенс угла1011. Ответьте на вопросы: а) Может ли абсцисса точки единичной полуокружности иметь значения 0,3; 1012. Проверьте, что точки M1 (0; 1), 1013.
1014. Найдите cos α, если:
1015. а) cos α = 1; г) 1016. 1017. Постройте ∠A, если:
1018. а) ОА = 3, α = 45°; б) ОА = 1,5, α = 90°; в) ОА = 5, α = 150°;
1019. Найдите угол между лучом ОА и положительной полуосью Ох, если точка А имеет координаты: а) (2; 2); б) (0; 3); в) (-√3; 1); г) (-2√2; 2√2). Ответы к задачам § 1. Синус, косинус, тангенс, котангенс угла1013. 1014. 1015. а) 0; 1016. 1018. 1019. а) 45°; б) 90°; в) 150°; г) 135°.
|
|
|



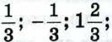 -2,8? б) Может ли ордината точки единичной полуокружности иметь значения 0,6;
-2,8? б) Может ли ордината точки единичной полуокружности иметь значения 0,6; 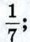 -0,3; 7; 1,002? Ответы обоснуйте.
-0,3; 7; 1,002? Ответы обоснуйте.
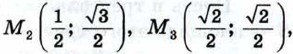
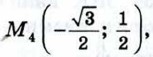 А (1; 0), В (-1; 0) лежат на единичной полуокружности. Выпишите значения синуса, косинуса и тангенса углов АОМ1, АОМ2, АОМ3, АОМ4, АОВ.
А (1; 0), В (-1; 0) лежат на единичной полуокружности. Выпишите значения синуса, косинуса и тангенса углов АОМ1, АОМ2, АОМ3, АОМ4, АОВ.
 Найдите sin α, если:
Найдите sin α, если:
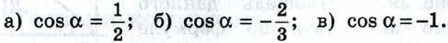
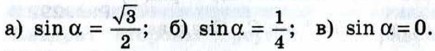
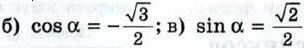 и 0° < α < 90°;
и 0° < α < 90°;
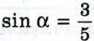 и 90° < α < 180°.
и 90° < α < 180°.
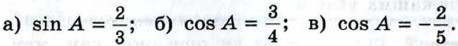
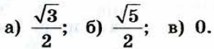
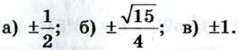
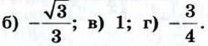
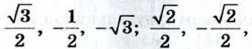 -1;
-1; 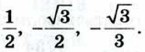
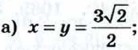 б) х = 0, у = 1,5; в)
б) х = 0, у = 1,5; в) 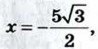 у = 2,5; г) х = -1, у = 0; д) х = ∠3, у = 1.
у = 2,5; г) х = -1, у = 0; д) х = ∠3, у = 1.