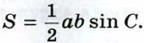Теорема о площади треугольника

Теорема

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Доказательство

Пусть в треугольнике АВС ВС = а, СА = b и S — площадь этого треугольника. Докажем, что

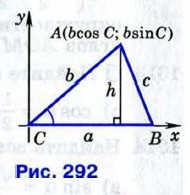
Рис. 292

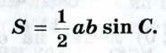
Введём систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси Сх, а точка А имела положительную ординату (рис. 292). Площадь данного треугольника можно вычислить по формуле 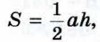где h — высота треугольника. Но h равна ординате точки А, т. е. h = b sin С. Следовательно,

Теорема доказана.