|
|
|
|
|
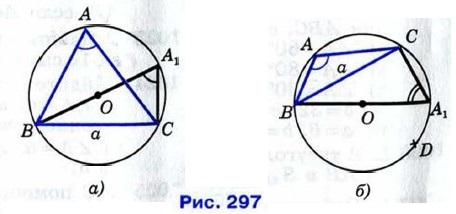
§ 2. Соотношения между сторонами и углами треугольника Задачи к § 2. Соотношения между сторонами и углами треугольника (продолжение)1033. Докажите, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Решение Пусть R — радиус окружности, описанной около треугольника АВС. Докажем, что Проведём диаметр ВА1 (рис. 297) и рассмотрим треугольник А1ВС (случай, когда точки А1 и С совпадают, рассмотрите самостоятельно). Угол С этого треугольника прямой, поэтому ВС = ВА1 • sin А1. Но sin А1 = sin А. Действительно, если точка A1 лежит на дуге ВАС (рис. 297, а), то ∠A1 = ∠A, а если на дуге BDC (рис. 297, б), то ∠A1 = 180° - ∠A. И в том, и в другом случае sin А1 = sin А. Следовательно, ВС = ВА1 • sin А, или ВС = 2R sin А.
1034. 1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острый угол между этими хордами, если АВ = 13см, СЕ = 9 см, ED = 4 см и расстояние между точками В и D равно 4√3 см. 1036.
1037. 1038.
|
|
|



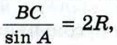 или BC = 2R sin А.
или BC = 2R sin А.
 В равнобедренной трапеции меньшее основание равно боковой стороне, большее основание равно 10 см, а угол при основании равен 70°. Найдите периметр трапеции.
В равнобедренной трапеции меньшее основание равно боковой стороне, большее основание равно 10 см, а угол при основании равен 70°. Найдите периметр трапеции.