|
|
§ 2. Соотношения между сторонами и углами треугольника



Задачи к § 2. Соотношения между сторонами и углами треугольника
1020.  Найдите площадь треугольника АВС, если: а) АВ = 6√8 см, АС = 4 см, ∠A = 60°; б) ВС = 3см, АВ = 18√;2 см, ∠B = 45°; в) АС = 14 см, СВ = 7 см, ∠C = 48°. Найдите площадь треугольника АВС, если: а) АВ = 6√8 см, АС = 4 см, ∠A = 60°; б) ВС = 3см, АВ = 18√;2 см, ∠B = 45°; в) АС = 14 см, СВ = 7 см, ∠C = 48°.
1021. Докажите, что площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
1022.  Площадь треугольника АВС равна 60 см2. Найдите сторону АВ, если АС = 15 см, ∠A = 30°. Площадь треугольника АВС равна 60 см2. Найдите сторону АВ, если АС = 15 см, ∠A = 30°.
1023.  Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями равен 30°. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями равен 30°.
1024. Найдите площадь треугольника АВС, если:
а) ∠A = α, а высоты, проведённые из вершин В и С, соответственно равны hb и hc;
б) ∠A = α, ∠B = β, а высота, проведённая из вершины В, равна h.
1025.  С помощью теорем синусов и косинусов решите треугольник АВС, если: С помощью теорем синусов и косинусов решите треугольник АВС, если:
a) ∠A = 60°, ∠B = 40°, с = 14;
б) ∠A = 30°, ∠C = 75°, 6 = 4,5;
в) ∠A = 80°, а = 16, b = 10;
г) ∠B = 45°, ∠C = 70°, а = 24,6;
д) ∠A = 60°, а = 10, b = 7;
е) а = 6,3, 6 = 6,3, ∠C = 54°;
ж) 6 = 32, с = 45, ∠A = 87°;
з) а = 14, 6 = 18, с = 20;
и) а = 6, b = 7,3, с = 4,8.
1026.  В треугольнике АВС АС= 12 см, ∠A- 75°, ∠C = 60°. Найдите АВ и SABC. В треугольнике АВС АС= 12 см, ∠A- 75°, ∠C = 60°. Найдите АВ и SABC.
1027.  Найдите стороны треугольника АВС, если ∠A = 45°, ∠C = 30°, а высота AD равна 3 м. Найдите стороны треугольника АВС, если ∠A = 45°, ∠C = 30°, а высота AD равна 3 м.
1028.  В параллелограмме ABCD В параллелограмме ABCD 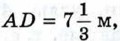 BD = 4,4 м, А А = 22°30'. BD = 4,4 м, А А = 22°30'.
1029. Найдите биссектрисы треугольника, если одна из его сторон равна а, а прилежащие к этой стороне углы равны α и β.
1030. Смежные стороны параллелограмма равны а и b, а один из его углов равен а. Найдите диагонали параллелограмма и угол между ними.
1031.  Выясните, является ли треугольник остроугольным, прямоугольным или тупоугольным, если его стороны равны: а) 5, 4 и 4; б) 17, 8 и 15; в) 9, 5 и 6. Выясните, является ли треугольник остроугольным, прямоугольным или тупоугольным, если его стороны равны: а) 5, 4 и 4; б) 17, 8 и 15; в) 9, 5 и 6.
1032.  Две равные по величине силы приложены к одной точке под углом 72° друг к другу. Найдите величины этих сил, если величина их равнодействующей равна 120 кг. Две равные по величине силы приложены к одной точке под углом 72° друг к другу. Найдите величины этих сил, если величина их равнодействующей равна 120 кг.
Продолжение >>>
|



 Найдите площадь треугольника АВС, если: а) АВ = 6√8 см, АС = 4 см, ∠A = 60°; б) ВС = 3см, АВ = 18√;2 см, ∠B = 45°; в) АС = 14 см, СВ = 7 см, ∠C = 48°.
Найдите площадь треугольника АВС, если: а) АВ = 6√8 см, АС = 4 см, ∠A = 60°; б) ВС = 3см, АВ = 18√;2 см, ∠B = 45°; в) АС = 14 см, СВ = 7 см, ∠C = 48°.
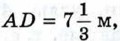 BD = 4,4 м, А А = 22°30'.
BD = 4,4 м, А А = 22°30'.