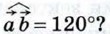|
|
Глава XI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов



Дополнительные задачи к главе XI
1057. В равнобедренном треугольнике ABC АВ = AC = b, ∠A = 30°. Найдите высоты BE и AD, а также отрезки АЕ, ЕС, ВС.
1058.  Найдите площадь треугольника АВС, если: Найдите площадь треугольника АВС, если:
а) ВС = 4,125 м, ∠B = 44°, ∠C=72°;
б) ВС = 4100 м, ∠A = 32°, ∠C = 120°.
1059. Докажите, что площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
1060.  Используя теорему синусов, решите треугольник АВС, если: Используя теорему синусов, решите треугольник АВС, если:
а) АВ = 8 см, ∠A = 30°, ∠B = 45°;
б) АВ = 5 см, ∠B = 45°, ∠C = 60°;
в) АВ = Зсм, ВС = 3,3 см, ∠A = 48°30';
г) АС = 10,4 см, ВС = 5,2 см, ∠B = 62°48'.
1061.  Используя теорему косинусов, решите треугольник АВС, если: Используя теорему косинусов, решите треугольник АВС, если:
а) АВ = 5 см, АС = 7,5 см, ∠A = 135°;
б) АВ - 2√2 дм, ВС = 3 дм, ∠B = 45°;
в) АС = 0,6 м, 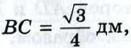 ∠C = 150°. ∠C = 150°.
1062.  В треугольнике DEF DE = 4,5 дм, .ЕВ = 9,9 дм, DF = 70 см. Найдите углы треугольника. В треугольнике DEF DE = 4,5 дм, .ЕВ = 9,9 дм, DF = 70 см. Найдите углы треугольника.
1063. Найдите биссектрису AD треугольника АВС, если ∠A = a, АВ = с, АС = b.
1064. Чтобы определить расстояние между точками А и В, которое нельзя измерить, выбирают третью точку С, из которой видны точки А и В. Измерив угол АСВ и расстояния АС и СВ, находят расстояние АВ. Найдите АВ, если AC = b, СВ = а, ∠ACB = a.
1065.  Докажите, что треугольник с вершинами А (3; 0), В (1; 5) и С (2; 1) тупоугольный. Найдите косинус тупого угла. Докажите, что треугольник с вершинами А (3; 0), В (1; 5) и С (2; 1) тупоугольный. Найдите косинус тупого угла.
1066.  Найдите длину вектора Найдите длину вектора  = 3 = 3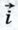 -4 -4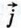 , где , где 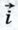 и и 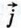 — координатные векторы. — координатные векторы.
1067.  Найдите диагонали параллелограмма, построенного на векторах Найдите диагонали параллелограмма, построенного на векторах 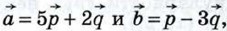 если если 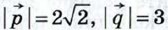 и и 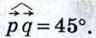
1068.  При каком значении х векторы При каком значении х векторы 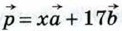 и и 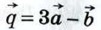 перпендикулярны, если | перпендикулярны, если | | = 2, | | = 2, | | = 5 и | = 5 и 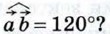
1069.  В прямоугольном равнобедренном треугольнике проведены медианы из вершин острых углов. Найдите острый угол между этими медианами. В прямоугольном равнобедренном треугольнике проведены медианы из вершин острых углов. Найдите острый угол между этими медианами.
1070.  В трапеции ABCD с основаниями АО= 16 см и ВС = 8 см боковая сторона равна 4√7 см, a ∠ADC = 60°. Через вершину С проведена прямая l, делящая трапецию на два многоугольника, площади которых равны. Найдите площадь трапеции и длину отрезка прямой l, заключённого внутри трапеции. В трапеции ABCD с основаниями АО= 16 см и ВС = 8 см боковая сторона равна 4√7 см, a ∠ADC = 60°. Через вершину С проведена прямая l, делящая трапецию на два многоугольника, площади которых равны. Найдите площадь трапеции и длину отрезка прямой l, заключённого внутри трапеции.
1071.  В треугольнике АВС, площадь которого равна 3√3, угол А острый, АВ = 4√3, АС = 3. Найдите радиус окружности, описанной около треугольника. В треугольнике АВС, площадь которого равна 3√3, угол А острый, АВ = 4√3, АС = 3. Найдите радиус окружности, описанной около треугольника.
1072.  Дан ромб MNPQ. Отрезок MF — биссектриса треугольника MPQ, ∠NMQ = 4α, FQ = a. Найдите площадь данного ромба. Дан ромб MNPQ. Отрезок MF — биссектриса треугольника MPQ, ∠NMQ = 4α, FQ = a. Найдите площадь данного ромба.
Продолжение >>>
|



 Найдите площадь треугольника АВС, если:
Найдите площадь треугольника АВС, если:
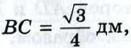 ∠C = 150°.
∠C = 150°.
 = 3
= 3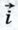 -4
-4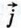 , где
, где 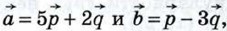 если
если 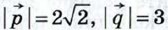 и
и 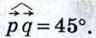
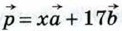 и
и 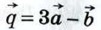 перпендикулярны, если |
перпендикулярны, если | | = 5 и
| = 5 и