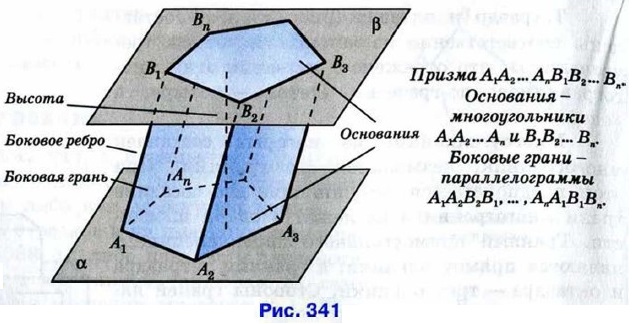
Призма

Многогранник, называемый призмой, можно построить следующим образом. Рассмотрим параллельные плоскости α и β, т. е. такие плоскости, которые не имеют общих точек. В плоскости а возьмём какой-нибудь многоугольник A₁A₂...A_n, а в плоскости β— равный ему многоугольник В₁В₂...В_n, причём так, чтобы равные стороны А₁А₂ и В₁В₂, А₂А₃ и В₂В₃, ..., А_nА₁ и В_nВ₁ этих многоугольников были параллельными сторонами четырёхугольников А₁А₂В₂В₁, А₂А₃В₃В₂, ..., А_nА₁В₁В_n (рис. 341).

Рис. 341

Поясним, что понимается под параллельностью прямых в пространстве. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Указанные четырёхугольники являются параллелограммами. В самом деле, например, в четырёхугольнике А₁А₂В₂В₁ противоположные стороны А₁А₂ и В₁В₂ по построению равны и параллельны, поэтому этот четырёхугольник — параллелограмм

n-угольной призмой называется многогранник А₁А₂...А_nВ₁В₂...В_n, составленный из двух равных л-угольников А₁А₂...А_n и В₁В₂...В_n — оснований призмы и n параллелограммов А₁А₂В₂В₁, ..., А_nА₁В₁В_n — боковых граней призмы. Отрезки А₁В₁, ..., А_nВ_n называются боковыми рёбрами призмы. Все они равны и параллельны друг другу.

Окончание >>>