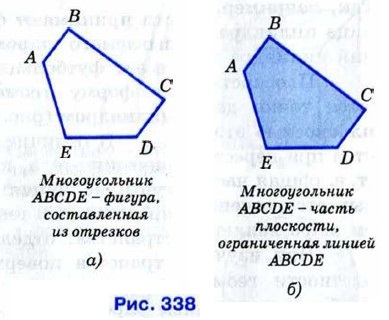
Многогранник

Напомним, что в планиметрии при изучении многоугольников мы рассматривали многоугольник либо как замкнутую линию, составленную из отрезков и не имеющую самопересечений (рис. 338, а), либо как часть плоскости, ограниченную этой линией, включая её саму (рис. 338, б). При изучении многогранников мы будем пользоваться вторым толкованием многоугольника.

Рис. 338

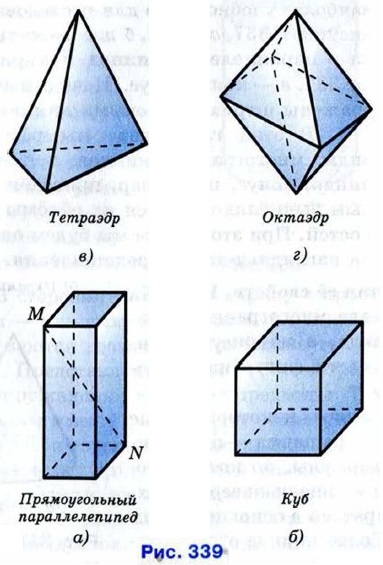
С одним из самых простых многогранников — прямоугольным параллелепипедом — вы знакомы давно. Этот многогранник составлен из шести прямоугольников (рис. 339, а). Форму прямоугольного параллелепипеда имеют коробки, комнаты и многие другие предметы. На рисунках 339, б, в, г изображены другие многогранники: куб (это прямоугольный параллелепипед, составленный из шести равных квадратов), тетраэдр, октаэдр.

Рис. 339

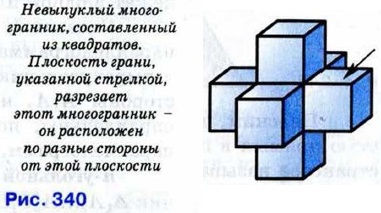
Можно сказать, что многогранник — это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Это тело также называется многогранником.

Тетраэдр и октаэдр (рис. 339,в, г) составлены соответственно из четырёх и восьми треугольников, что отражено в названии этих многогранников: по-гречески «тетра» — четыре, а «окто» — восемь.

Многоугольники, из которых составлен многогранник, называются его гранями. При этом предполагается, что никакие две соседние грани многогранника не лежат в одной плоскости. Гранями прямоугольного параллелепипеда являются прямоугольники, а гранями тетраэдра и октаэдра — треугольники. Стороны граней называются рёбрами, а концы рёбер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника. На рисунке 339, а отрезок MN — диагональ прямоугольного параллелепипеда.

Многогранники бывают выпуклыми и невыпуклыми. Выпуклый многогранник характеризуется тем, что он расположен по одну сторону от плоскости каждой своей грани. На рисунке 339 изображены выпуклые многогранники, а на рисунке 340 — невыпуклый многогранник.

Рис. 340