|
|
|
|
|
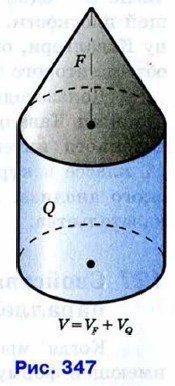
§ 1. Многогранники Объём тела (окончание)Рассмотрим тело, составленное из нескольких тел так, что внутренние области этих тел не имеют общих точек (рис. 347). Ясно, что объём всего тела складывается из объёмов составляющих его тел. Итак,
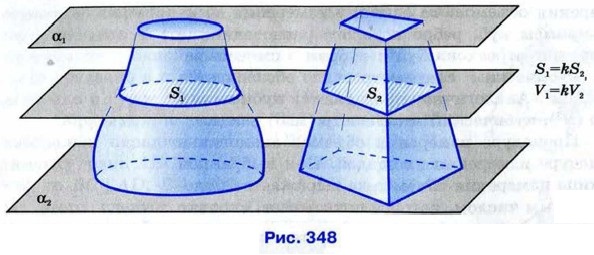
Свойства 10 и 20 называются основными свойствами объёмов. Напомним, что аналогичными свойствами обладают длины отрезков и площади многоугольников. Для нахождения объёмов тел в ряде случаев удобно пользоваться теоремой, получившей название принцип Кавальери1. 1 Кавальери Бонавентура (1598—1647) — итальянский математик.
Доказательство теоремы, выражающей принцип Кавальери, основано на понятии определённого интеграла, которое будет введено в 11 классе в курсе алгебры и начал математического анализа. Мы примем эту теорему без доказательства.
|
|
|