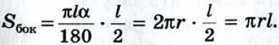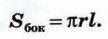|
|
|
|
|
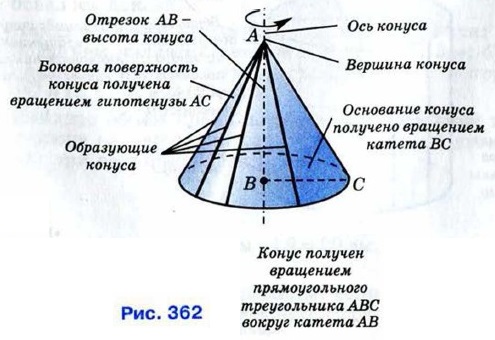
§ 2. Тела и поверхности вращения КонусВозьмём прямоугольный треугольник АВС и будем вращать его вокруг катета АВ (рис. 362). В результате получится тело, которое называется конусом. Прямая АВ называется осью конуса, а отрезок АВ — его высотой. При вращении катета ВС образуется круг, он называется основанием конуса. При вращении гипотенузы АС образуется поверхность, состоящая из отрезков с общим кондом А. Её называют конической поверхностью или боковой поверхностью конуса, а отрезки, из которых она составлена, — образующими конуса. Таким образом, конус — это тело, ограниченное кругом и конической поверхностью.
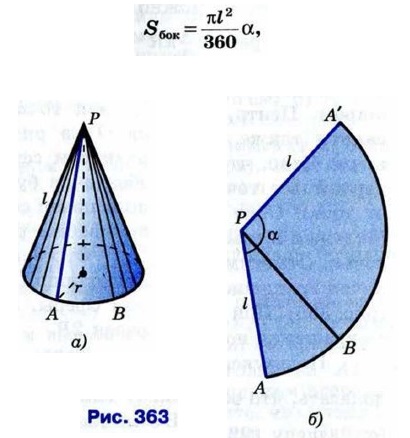
Пользуясь принципом Кавальери, можно доказать (см. задачу 1219), что объём конуса равен одной трети произведения площади основания на высоту. Иначе говоря, объём V конуса выражается формулой Рассмотрим теперь конус, у которого радиус основания равен r, а образующая равна l (рис. 363, а). Его боковую поверхность можно развернуть на плоскость, разрезав её по одной из образующих. Развёртка боковой поверхности конуса представляет собой круговой сектор (рис. 363, б). Радиус этого сектора равен образующей конуса, т. е. равен l, а длина дуги сектора равна длине окружности основания конуса, т. е. равна 2πr. Площадь Sбок боковой поверхности конуса равна площади её развёртки, т. е.
где α — градусная мера дуги сектора (см. рис. 363, б). Длина дуги окружности с градусной мерой а и радиусом l равна Итак, площадь боковой поверхности конуса с образующей l и радиусом основания r выражается формулой:
|
|
|



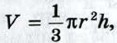 где r — радиус основания конуса, h — его высота.
где r — радиус основания конуса, h — его высота.
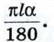 С другой стороны, длина этой дуги равна 2 πr, т. е.
С другой стороны, длина этой дуги равна 2 πr, т. е. 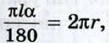 поэтому
поэтому