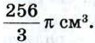|
|
|
|
|
§ 2. Тела и поверхности вращения Ответы к задачам § 2. Тела и поверхности вращения1226. Пусть V — объём шара радиуса R, S — площадь его поверхности. Найдите: a) S и V, если R = 4см; б) R и S, если V = 113,04 см3; в) R и V, если S = 64π см2. 1227. Диаметр Луны составляет (приближённо) четвёртую часть диаметра Земли. Сравните объёмы Луны и Земли, считая их шарами. 1228. Стаканчик для мороженого конической формы имеет глубину 12 см и диаметр верхней части 5 см. На него сверху положили две ложки мороженого в виде полушарий диаметром 5 см. Переполнит ли мороженое стаканчик, если оно растает? 1229. Сколько кожи пойдёт на покрышку футбольного мяча радиуса 10 см (на швы добавить 8% от площади поверхности мяча)? 1230. Докажите, что площадь сферы равна площади полной поверхности конуса, высота которого равна диаметру сферы, а диаметр основания равен образующей конуса. 1231. Отношение объёмов двух шаров равно 8. Как относятся площади их поверхностей? Ответы к задачам § 2. Тела и поверхности вращения1214. а) 24π см3; 1215. 1216. π2м2. 1217. ≈ 2,58 м2. 1218. 1220. а) 2,25π см3; б) 9см; 1221. 1222. 1223. Sбок = 80π см2, Sкон = 144π см2. 1226. а) 64π см2, 1227. Объём Земли в 64 раза больше объёма Луны. 1228. Нет. 1229. 432π см2 ≈ 1357см2. 1231. 4 : 1.
|
|
|



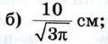 в) 2 см.
в) 2 см.
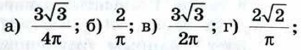
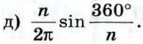
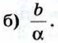

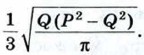
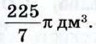
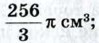 б) ≈ 3 см, ≈ 36л см2; в) 4 см,
б) ≈ 3 см, ≈ 36л см2; в) 4 см,