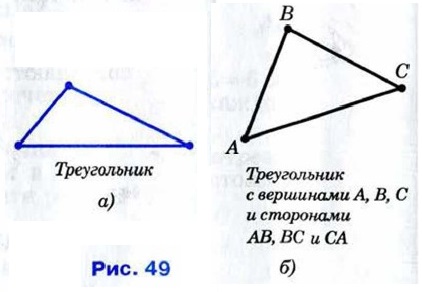
Треугольник

В этой главе вы начнёте изучение свойств треугольников и окружностей. Треугольник — одна из самых простых и вместе с тем самых важных фигур в геометрии. То же самое можно сказать об окружности. Оказывается, что эти простые фигуры таят в себе много интересного и неожиданного. Различные их свойства вы будете изучать на протяжении всего курса геометрии. При этом мы будем формулировать и доказывать теоремы. Что такое теорема и что значит доказать теорему, вы узнаете в данной главе, где появятся первые теоремы о треугольниках.

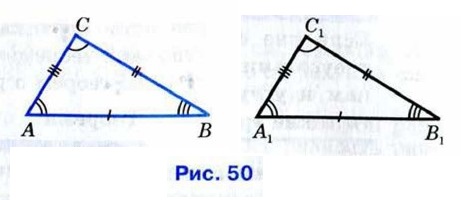
Отметим какие-нибудь три точки, не лежащие на одной прямой, и соединим их отрезками (рис. 49, а). Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки называются вершинами, а отрезки — сторонами треугольника. На рисунке 49, б изображён треугольник с вершинами А, В, С и сторонами АВ, ВС и С А. Такой треугольник будем обозначать так: АВС (читается: «треугольник АВС»). Этот же треугольник можно обозначить иначе, записав буквы А, В, С в другом порядке: ВСА, СВА и т. д.

Треугольник

Три угла — ∠ВАС, ∠СВА и ∠АСВ — называются углами треугольника АВС. Часто их обозначают одной буквой: ∠А, ∠В, ∠С.

Сумма длин трёх сторон треугольника называется его периметром.

Напомним, что две фигуры, в частности два треугольника, называются равными, если их можно совместить наложением. На рисунке 50 изображены равные треугольники АВС и А₁В₁С₁.

Окончание >>>