|
§ 2. Медианы, биссектрисы и высоты треугольника



Задачи к § 2. Медианы
105.  Точки А и С лежат по одну сторону от прямой а. Перпендикуляры АВ и CD к прямой а равны. Точки А и С лежат по одну сторону от прямой а. Перпендикуляры АВ и CD к прямой а равны.
а) Докажите, что ∠ABD = ∠CDB;
б) найдите ∠ABC, если ∠ADB = 44°.
106.  Медиана AD треугольника АВС продолжена за точку D на отрезок DE, равный AD, и точка Е соединена с точкой С. Медиана AD треугольника АВС продолжена за точку D на отрезок DE, равный AD, и точка Е соединена с точкой С.
а) Докажите, что AABD = AECD;
б) найдите ∠ACE, если ∠ACD = 56°, ∠ABD = 40°.
107.  В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр равен 50 см. Найдите стороны треугольника. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр равен 50 см. Найдите стороны треугольника.
108.  Периметр равнобедренного треугольника АВС с основанием ВС равен 40 см, а периметр равностороннего треугольника BCD равен 45 см. Найдите стороны АВ и ВС. Периметр равнобедренного треугольника АВС с основанием ВС равен 40 см, а периметр равностороннего треугольника BCD равен 45 см. Найдите стороны АВ и ВС.
109.  В равнобедренном треугольнике АВС с основанием ВС проведена медиана AM. Найдите медиану AM, если периметр треугольника АВС равен 32 см, а периметр треугольника АВМ равен 24 см. В равнобедренном треугольнике АВС с основанием ВС проведена медиана AM. Найдите медиану AM, если периметр треугольника АВС равен 32 см, а периметр треугольника АВМ равен 24 см.
110.  Докажите, что если медиана треугольника является его высотой, то треугольник равнобедренный. Докажите, что если медиана треугольника является его высотой, то треугольник равнобедренный.
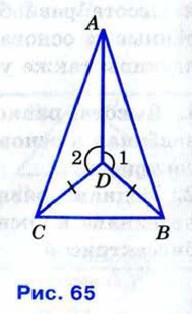
111.  На рисунке 65 CD = BD, ∠1 =∠2. Докажите, что треугольник АВС равнобедренный. На рисунке 65 CD = BD, ∠1 =∠2. Докажите, что треугольник АВС равнобедренный.
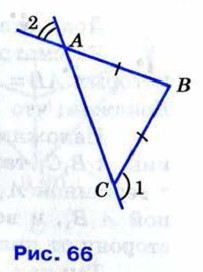
112.  На рисунке 66 АВ = ВС, ∠1 = 130°. Найдите ∠2. На рисунке 66 АВ = ВС, ∠1 = 130°. Найдите ∠2.
113. Точки М и Р лежат по одну сторону от прямой b. Перпендикуляры MN и PQ, проведённые к прямой b, равны. Точка О — середина отрезка NQ.
а) Докажите, что ∠OMP = ∠OPM;
б) найдите ∠NOM, если ∠MOP = 105°.
114.  Докажите, что в равных треугольниках медианы, проведённые к равным сторонам, равны. Докажите, что в равных треугольниках медианы, проведённые к равным сторонам, равны.
Окончание >>>
| 


 Точки А и С лежат по одну сторону от прямой а. Перпендикуляры АВ и CD к прямой а равны.
Точки А и С лежат по одну сторону от прямой а. Перпендикуляры АВ и CD к прямой а равны.