|
|
|
|
|
§ 3. Второй и третий признаки равенства треугольников Задачи к § 3. Второй и третий признаки равенства треугольников121. а) Докажите, что 122. а) Докажите, что 123. 124.
125.
126. 127. В треугольниках АВС и А1B1С1 АВ = А1В1, ВС = B1C1, ∠B — ∠B1. На сторонах АВ и A1B1 отмечены точки D и D1 так, что ∠ACO = ∠A1C1D1. Докажите, что 128. Докажите, что в равных треугольниках биссектрисы, проведённые к соответственно равным сторонам, равны. 129. Отрезки АС и BD пересекаются в середине О отрезка АС, ∠BCO = ∠DAO. Докажите, что 130. В треугольниках АВС и A1В1С1 отрезки СО и С1О1 — медианы, BC = B1C1, ∠B — ∠B1 и ∠C = ∠C1. Докажите, что: а) 131. В треугольниках DEF и MNP EF — NP, DF = MP и ∠F = ∠P. Биссектрисы углов Е и D пересекаются в точке О, а биссектрисы углов М и N — в точке К. Докажите, что ∠DOE = ∠MKN. 132. Прямая, перпендикулярная к биссектрисе угла А, пересекает стороны угла в точках М и N. Докажите, что треугольник AMN — равнобедренный. 133. Докажите, что если биссектриса треугольника является его высотой, то треугольник — равнобедренный. 134. Докажите, что равнобедренные треугольники равны, если основание и прилежащий к нему угол одного треугольника соответственно равны основанию и прилежащему к нему углу другого треугольника.
|
|
|



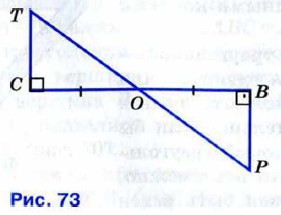
 Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC.
Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC.
 СВО =
СВО =