Главная >> Геометрия 7—9 классы. Атанасян

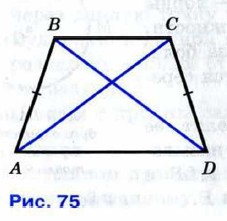
§ 3. Второй и третий признаки равенства треугольников

Задачи к § 3. Второй и третий признаки равенства треугольников (ответы)

135. Докажите, что если сторона одного равностороннего треугольника равна стороне другого равностороннего треугольника, то треугольники равны.

136. На рисунке 52 (см. с. 31) АВ-АС, BD = DC и ∠BAC = 50°. Найдите ∠CAD.

137. На рисунке 53 (см. с. 31) BC = AD, AB = CD. Докажите, что ∠B = ∠D.

138. На рисунке 75 AB = CD и BD = АС. Докажите, что: a) ∠CAD = ∠ADB; б) ∠BAC = ∠CDB.

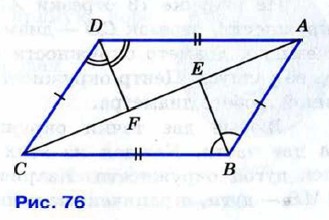
139. На рисунке 76 AB = CD, AD = BC, BE — биссектриса угла ABC, a DF — биссектриса угла ADC. Докажите, что:

а) ∠ABE = ∠ADF;
б) АВЕ = CDF.

140. В треугольниках АВС и А₁В₁С₁ медианы ВМ и В₁М₁ равны, АВ = А₁В₁ АС = А₁С₁. Докажите, что АВС = А₁В₁С₁.

141. В треугольниках АВС и А₁В₁С₁ отрезки AD и A₁D₁ — биссектрисы, АВ = А₁В₁, BD = B₁D₁ и AD = A₁D₁. Докажите, что АВС = А₁В₁С₁.

142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезок CD в точке О. Докажите, что: a) ∠ADB = ∠ACB; б) DO = OC.

Ответы к задачам § 3. Второй и третий признаки равенства треугольников

121. б) ВС = 15 см, СО = 13 см.

122. б) АВ = 11 см, ВС =19см.

126. 13см.

136. 25°.

142. Указание. Рассмотреть два случая. Точка В лежит: а) на луче АО; б) на продолжении луча АО.

<<< К началу