Главная >> Геометрия 7—9 классы. Атанасян

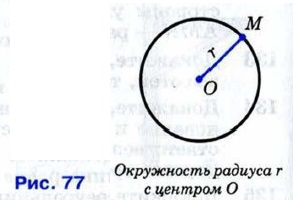
§ 4. Задачи на построение

Окружность

Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением. Мы уже встречались с определениями, например с определением угла, смежных углов, равнобедренного треугольника и т. д. Дадим определение ещё одной геометрической фигуры — окружности.

Определение

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности (рис. 77). Из определения окружности следует, что все радиусы имеют одну и ту же длину.

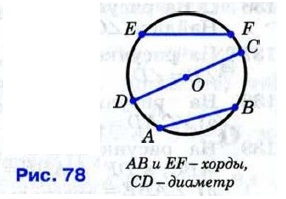
Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется её диаметром.

На рисунке 78 отрезки АВ и EF — хорды окружности, отрезок CD — диаметр окружности. Очевидно, диаметр окружности в два раза больше её радиуса. Центр окружности является серединой любого диаметра.

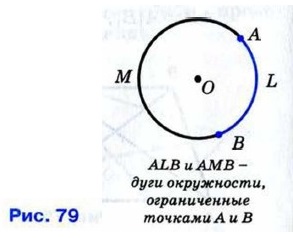
Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. На рисунке 79 ALB и АМВ — дуги, ограниченные точками А и В.

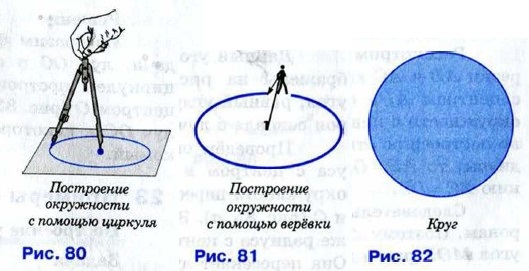
Для изображения окружности на чертеже пользуются циркулем (рис. 80). Чтобы провести окружность на местности, можно воспользоваться верёвкой (рис. 81).

Часть плоскости, ограниченная окружностью, называется кругом (рис. 82).