|
|
|
|
|
§ 1. Признаки параллельности двух прямых Признаки параллельности двух прямых (окончание)Теорема
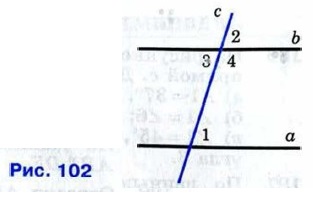
Доказательство Пусть при пересечении прямых а и b секущей с соответственные углы равны, например ∠1 =∠2 (рис. 102). Так как углы 2 и 3 — вертикальные, то ∠2 = ∠3. Из этих двух равенств следует, что ∠1 = ∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые а и b параллельны. Теорема доказана.
Теорема
Доказательство Пусть при пересечении прямых а и b секущей с сумма односторонних углов равна 180°, например ∠1 + ∠4 = 180° (см. рис. 102). Так как углы 3 и 4 — смежные, то ∠3 + ∠4 = 180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые а и b параллельны. Теорема доказана.
|
|
|