|
|
|
|
|
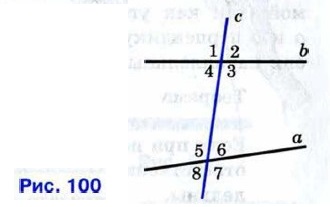
§ 1. Признаки параллельности двух прямых Признаки параллельности двух прямыхПрямая с называется секущей по отношению к прямым а и b, если она пересекает их в двух точках (рис. 100). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 100 обозначены цифрами. Некоторые пары этих углов имеют специальные названия: накрест лежащие углы: 3 и 5, 4 и 6;
Рассмотрим три признака параллельности двух прямых, связанные с этими парами углов. Теорема
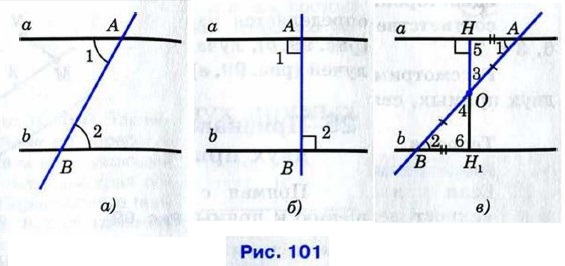
Доказательство Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны: ∠1 = ∠2 (рис. 101, а). Докажем, что а || b. Если углы 1 и 2 прямые (рис. 101, б), то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны. Рассмотрим случай, когда углы 1 и 2 не прямые. Из середины О отрезка АВ проведём перпендикуляр ОН к прямой а (рис. 101, в). На прямой b от точки В отложим отрезок ВН1, равный отрезку АН, как показано на рисунке 101, в, и проведём отрезок ОН1. Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними (АО = ВО, АН = ВН1, ∠1 = ∠2), поэтому ∠3 = ∠4 и ∠5 = ∠6. Из равенства ∠3 = ∠4 следует, что точка Н1 лежит на продолжении луча ОН, т. е. точки Н, О и Н1 лежат на одной прямой, а из равенства ∠5 = ∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Итак, прямые а и b перпендикулярны к прямой HH1 поэтому они параллельны. Теорема доказана.
|
|
|