|
|
|
|
|
§ 2. Соотношения между сторонами и углами треугольника Некоторые свойства прямоугольных треугольниковРассмотрим свойства прямоугольных треугольников, которые устанавливаются с помощью теоремы о сумме углов треугольника.
В самом деле, сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника равна 90°.
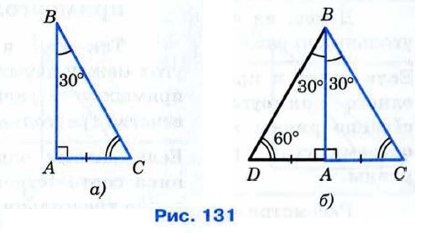
Рассмотрим прямоугольный треугольник АВС, в котором угол А — прямой, ∠B = 30° и, значит, ∠C = 60° (рис. 131, а). Докажем, что Приложим к треугольнику АВС равный ему треугольник ABD так, как показано на рисунке 131, б. Получим треугольник BCD, в котором ∠B = ∠D = 60°, поэтому DC = BC. Но
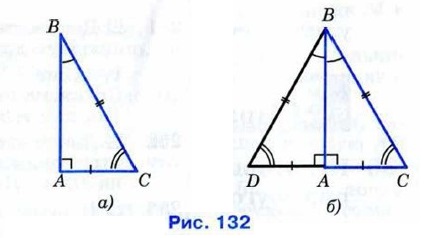
Рассмотрим прямоугольный треугольник АВС, у которого катет АС равен половине гипотенузы ВС (рис. 132, а). Докажем, что ∠ABC = 30°. Приложим к треугольнику АВС равный ему треугольник ABD так, как показано на рисунке 132, б. Получим равносторонний треугольник BCD. Углы равностороннего треугольника равны друг другу (объясните почему), поэтому каждый из них равен 60°. В частности, ∠DBC = 60°. Но ∠DBC = 2∠ABC. Следовательно, ∠ABC = 30°, что и требовалось доказать.
|
|
|



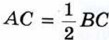 .
.
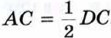 . Следовательно,
. Следовательно,