|
|
|
|
|
§ 2. Соотношения между сторонами и углами треугольника Признаки равенства прямоугольных треугольниковТак как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует:
Далее, из второго признака равенства треугольников следует:
Рассмотрим ещё два признака равенства прямоугольных треугольников. Теорема
Доказательство Из свойства 10 п. 35 следует, что в таких треугольниках два других острых угла также равны, поэтому треугольники равны по второму признаку равенства треугольников, т. е. по стороне (гипотенузе) и двум прилежащим к ней углам. Теорема доказана. Теорема
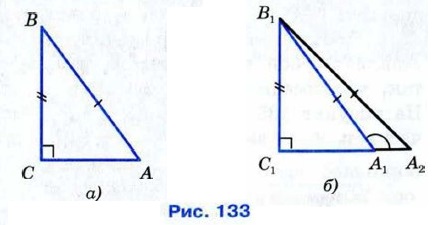
Доказательство Рассмотрим треугольники АBС и А1B1С1, у которых углы С и C1 — прямые, АB = А1B1, BС = B1С1 (рис. 133, а, б). Докажем, что
Так как ∠C = ∠Csub>1, то треугольник АВС можно наложить на треугольник А1B1С1 так, что вершина С совместится с вершиной С1, а стороны СА и СВ наложатся соответственно на лучи С1А1 и С1B1. Поскольку СB = С1B1, то вершина B совместится с вершиной B1. Но тогда вершины А и А1 также совместятся. В самом деле, если предположить, что точка А совместится с некоторой другой точкой А2 луча С1А1, то получим равнобедренный треугольник А1В1А2, в котором углы при основании А1А2 не равны (на рисунке 133, б ∠A2 — острый, a ∠A1 — тупой как смежный с острым углом В1А1С1). Но это невозможно, поэтому вершины А и А1 совместятся. Следовательно, полностью совместятся треугольники АВС и А1В1С1, т. е. они равны. Теорема доказана.
|
|
|



 АВС =
АВС =