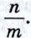|
|
|
|
|
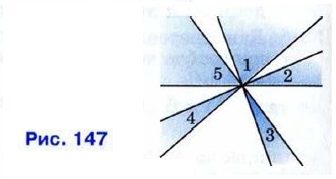
Задачи повышенной трудности Задачи повышенной трудности к главе I. Начальные геометрические сведения322. Пусть а — число, выражающее длину отрезка АВ при единице измерения CD, а b — число, выражающее длину отрезка CD при единице измерения АВ. Как связаны между собой числа а и b? 323. Длина отрезка АВ при единице измерения E1F1 выражается числом т, а при единице измерения E2F2 — числом n. Каким числом выражается длина отрезка E1F1 при единице измерения E2F2? 324. Пусть ∠hk — меньший из двух смежных углов hk и hl. Докажите, что
325.
326. Даны шесть попарно пересекающихся прямых. Известно, что через точку пересечения любых двух прямых проходит по крайней мере ещё одна из данных прямых. Докажите, что все эти прямые проходят через одну точку. 327. Даны шесть точек. Известно, что прямая, проходящая через любые две точки, содержит по крайней мере ещё одну из данных точек. Докажите, что все эти точки лежат на одной прямой. Ответы к задачам322. ab= 1. 323. 324. Указание. Воспользоваться свойством смежных углов: ∠hk + ∠hl = 180°. 325. 180°. 326. Указание. Пусть три из данных прямых проходят через точку А. Используя метод от противного, доказать, что каждая из оставшихся трёх прямых проходит через эту точку. 327. Указание. Пусть три из данных точек лежат на прямой d. Используя метод от противного, доказать, что каждая из оставшихся четырёх точек лежит на прямой d.
|
|
|



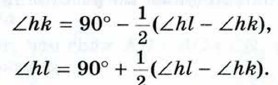
 Пять прямых пересекаются в одной точке (рис. 147). Найдите сумму углов 1, 2, 3, 4 и 5.
Пять прямых пересекаются в одной точке (рис. 147). Найдите сумму углов 1, 2, 3, 4 и 5.