|
|
|
|
|
§ 2. Параллелограмм и трапеция Задачи к § 2. Параллелограмм и трапеция371. a) ∠BAC = ∠ACD и ∠BCA = ∠D АС;
372. Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если: а) одна сторона на 3 см больше другой;
373. Периметр параллелограмма ABCD равен 50 см, ∠C = 30°, а перпендикуляр ВН к прямой CD равен 6,5 см. Найдите стороны параллелограмма. 374. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр этого параллелограмма, если ВК = 15 см, КС = 9 см. 375. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. 376. Найдите углы параллелограмм: ABCD, если: a) ∠A = 84°;
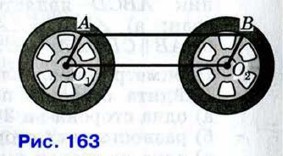
377. В параллелограмме MNPQ проведён перпендикуляр NH к прямой MQ, причём точка Н лежит на стороне MQ. Найдите стороны и углы параллелограмма, если известно, что МН = 3 см, HQ = 5 см, ∠MNH = 30°. 378. Докажите, что параллелограмм является выпуклым четырёхугольником. Решение Рассмотрим параллелограмм ABCD (см. рис. 157) и докажем, что он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Возьмём, например, прямую АВ. Отрезок CD не имеет общих точек с прямой АВ, так как АВ || CD. Значит, этот отрезок лежит по одну сторону от прямой АВ. Но тогда и отрезки ВС и AD лежат по ту же сторону от прямой АВ. Таким образом, параллелограмм ABCD лежит по одну сторону от прямой АВ. 379. 380. На сторонах АВ, ВС, CD и DA четырёхугольника ABCD отмечены соответственно точки М, N, Р и Q так, что АМ = СР, BN = DQ, BM = DP, NC = QA. Докажите, что ABCD и MNPQ — параллелограммы. 381. На рисунке 163 изображены два одинаковых колеса тепловоза. Радиусы О1А и О2В равны. Стержень АВ, длина которого равна расстоянию О1О2 между центрами колёс, передаёт движение от одного колеса к другому. Докажите, что отрезки АВ и О1О2 либо параллельны, либо лежат на одной прямой.
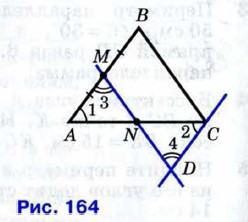
382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырёхугольник A1B1C1D1, вершинами которого являются середины отрезков ОА, ОВ, ОС и OD, — параллелограмм. 383. На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что РВ = QD. Докажите, что четырёхугольник APCQ — параллелограмм. 384. Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC. Решение Через точку С проведём прямую, параллельную прямой АВ, и обозначим буквой D точку пересечения этой прямой с прямой MN (рис. 164). Так как AM = МВ по условию, а МВ = CD как противоположные стороны параллелограмма BCDM, то AM = DC. Треугольники AMN и CDN равны по второму признаку равенства треугольников (AM = CD, ∠1=∠2 и ∠3 = ∠4 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущими АС и MD), поэтому AN = NC.
|
|
|



 Докажите, что выпуклый четырёхугольник ABCD является параллелограммом, если:
Докажите, что выпуклый четырёхугольник ABCD является параллелограммом, если: