Главная >> Геометрия 7—9 классы. Атанасян

§ 2. Площади параллелограмма, треугольника и трапеции

Площадь параллелограмма

Условимся одну из сторон параллелограмма называть основанием, а перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание, — высотой параллелограмма.

Теорема

Площадь параллелограмма равна произведению его основания на высоту.

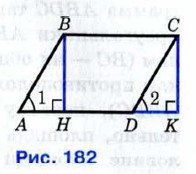
Доказательство

Рассмотрим параллелограмм ABCD с площадью S. Примем сторону AD за основание и проведём высоты ВН и СК (рис. 182). Докажем, что S = AD • ВН.

Докажем сначала, что площадь прямоугольника НВСК также равна S. Трапеция АВСК составлена из параллелограмма ABCD и треугольника DCK. С другой стороны, она составлена из прямоугольника НВСК и треугольника АВН. Но прямоугольные треугольники DCK и АВН равны по гипотенузе и острому углу (их гипотенузы АВ и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD), поэтому их площади равны.

Следовательно, площади параллелограмма ABCD и прямоугольника НВСК также равны, т. е. площадь прямоугольника НВСК равна S. По теореме о площади прямоугольника S = ВС • ВН, а так как ВС = AD, то S = AD • ВН. Теорема доказана.