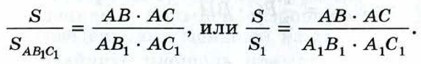|
|
|
|
|
§ 2. Площади параллелограмма, треугольника и трапеции Площадь треугольникаОдну из сторон треугольника часто называют его основанием. Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведённую к основанию. Теорема
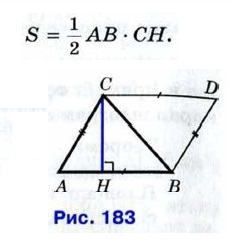
Доказательство Пусть S — площадь треугольника АВС (рис. 183). Примем сторону АВ за основание треугольника и проведём высоту СН. Докажем, что
Достроим треугольник АВС до параллелограмма ABDC так, как показано на рисунке 183. Треугольники АВС и DCB равны по трём сторонам (ВС — их общая сторона, АВ = CD и АС = BD как противоположные стороны параллелограмма ABDC), поэтому их площади равны. Следовательно, площадь S треугольника АВС равна половине площади параллелограмма ABDC, т. е. Следствие 1
Следствие 2
Воспользуемся следствием 2 для доказательства теоремы об отношении площадей треугольников, имеющих по равному углу. Теорема
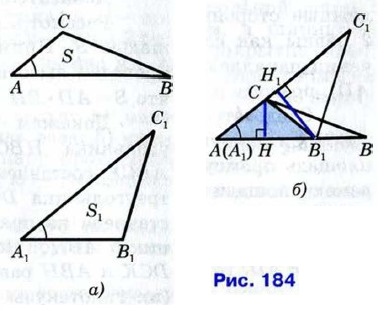
Доказательство Пусть S и S1 — площади треугольников АВС и A1B1C1, у которых ∠A = ∠A1 (рис. 184, а). Докажем, что
Наложим треугольник A1B1C1 на треугольник ABC так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и A1С1 наложились соответственно на лучи АВ и АС (рис. 184, б). Треугольники АВС и АВ1С имеют общую высоту — CН, поэтому
Теорема доказана.
|
|
|



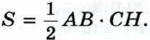 Теорема доказана.
Теорема доказана.
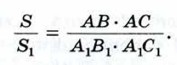
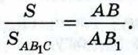 Треугольники АВ1С и АВ1С1 также имеют общую высоту — В1Н1, поэтому
Треугольники АВ1С и АВ1С1 также имеют общую высоту — В1Н1, поэтому 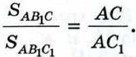 Перемножая полученные равенства, находим:
Перемножая полученные равенства, находим: