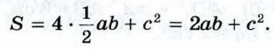|
|
|
|
|
§ 3. Теорема Пифагора Теорема ПифагораПользуясь свойствами площадей многоугольников, мы установим теперь замечательное соотношение между гипотенузой и катетами прямоугольного треугольника. Теорема, которую мы докажем, называется теоремой Пифагора. Она является важнейшей теоремой геометрии. Теорема
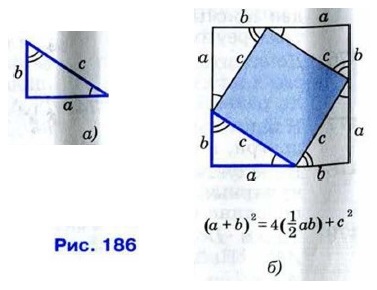
Доказательство Рассмотрим прямоугольный треугольник с катетами а, b и гипотенузой с (рис. 186, а). Докажем, что с2 = а2 + b2.
Достроим треугольник до квадрата со стороной а + b так, как показано на рисунке 186,6. Площадь S этого квадрата равна (a + b)2. С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь каждого из которых равна
Таким образом, (а + b)2 = 2аb + с2, откуда с2 = а2 + b2. Теорема доказана.
Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифа- гора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно, что тогда ещё не знали её доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор, по-видимому, нашёл доказательство этого соотношения. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам — даже сто быков. На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора. В настоящее время их насчитывается более ста. С одним из них мы уже познакомились, ещё с одним познакомимся в следующей главе (задача 578). Многие известные мыслители и писатели прошлого обращались к этой замечательной теореме и посвятили ей свои строки.
|
|
|



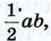 и квадрата со стороной с, поэтому
и квадрата со стороной с, поэтому