|
|
|
|
|
§ 3. Теорема Пифагора Теорема, обратная теореме ПифагораТеорема
Доказательство Пусть в треугольнике АВС АВ2 = АС2 + ВС2. Докажем, что угол С прямой. Рассмотрим прямоугольный треугольник А1В1С1 с прямым Углом С1, у которого А1С1 = АС и В1С1 = ВС. По теореме Пифагора Треугольники АВС и А1В1С1 равны по трём сторонам, поэтому ∠C = ∠C1, т. е. треугольник АВС прямоугольный с прямым углом С. Теорема доказана. По теореме, обратной теореме Пифагора, треугольник со сторонами 3, 4 и 5 является прямоугольным: 51 = 31 + 41. Прямоугольными являются также треугольники со сторонами 5, 12, 13; 8, 15, 17 и 7, 24, 25 (объясните почему). Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками. Можно доказать, что катеты а, b и гипотенуза с таких треугольников выражаются формулами a = 2k • m • n, b = k(m2 - n2), c = k(m2 + n2), где k, m и n — любые натуральные числа, такие, что m > n. Треугольник со сторонами 3, 4, 5 часто называют египетским треугольником, так как он был известен ещё древним египтянам. Для построения прямых углов египтяне поступали так: на верёвке делали метки, делящие её на 12 равных частей, связывали концы верёвки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Тогда угол между сторонами, равными 3 и 4, оказывался прямым.
|
|
|



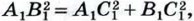 и, значит,
и, значит, 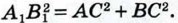 Но АС2 + ВС2 = АВ2 по условию теоремы. Следовательно,
Но АС2 + ВС2 = АВ2 по условию теоремы. Следовательно, 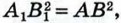 откуда А1В1 = АВ.
откуда А1В1 = АВ.