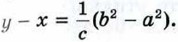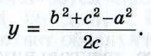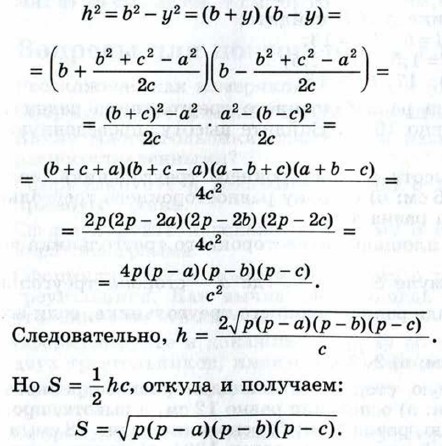|
|
|
|
|
§ 3. Теорема Пифагора Формула ГеронаТеорема
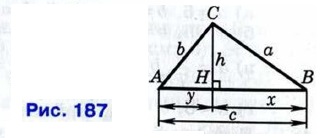
Доказательство Рассмотрим треугольник АВС, в котором AB = с, ВС = а, АС = b. В любом треугольнике по крайней мере два угла острые. Пусть А и В — острые углы треугольника АВС. Тогда основание Н высоты СН треугольника лежит на стороне АВ. Введём обозначения: CH = h, АН = у, НВ = х (рис. 187). По теореме Пифагора a2 - x2 = h2 = b2 - y2, откуда у2 - х2 = b2 - а2, или (у - х) (у + х) = b2 - а2. Так как у + х = с, то
Сложив два последних равенства и разделив на 2, получим:
Поэтому
Теорема доказана. Выведенную нами формулу обычно называют формулой Герона, по имени древнегреческого математика Герона Александрийского, жившего предположительно в I в. н. э.
|
|
|



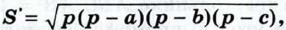 где
где 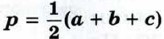 — полупериметр треугольника.
— полупериметр треугольника.