Главная >> Машиностроительное черчение. Инженерная графика. Чекмарев

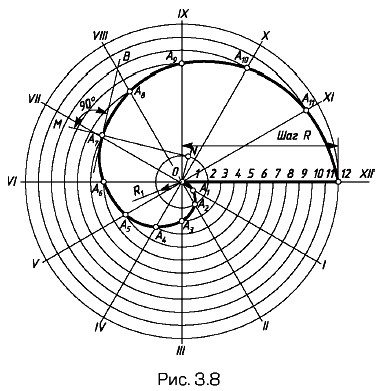
Кривые линии и их применение в чертежах

Построение спирали Архимеда

Построение спирали Архимеда. Траектория точки, равномерно передвигающейся по равномерно вращающемуся радиусу вокруг неподвижного центра, представляет собой плоскую кривую, называемую спиралью Архимеда. Расстояние между точками, лежащими на одном радиусе, называют шагом спирали. На это расстояние точка удаляется от центра при повороте на 360°. Спираль Архимеда имеет две ветви, одна из них образуется при вращении радиуса по часовой стрелке, вторая — против часовой. Построение спирали Архимеда при заданном шаге R показано на рис. 3.8. Окружность радиуса R и шаг спирали делят на одинаковое количество равных частей (например, на 12). Пересечение концентрических дуг, проведенных радиусами O1, O2, O3,... с лучами OI, OII, OIII,..., определяет точки А₁, А₂, А₃, ... спирали. Для построения касательной и нормали к любой точке используют окружность радиуса R₁ длина которой равна шагу R спирали. Касательная к окружности радиуса R₁ является нормалью к спирали в точке их пересечения, например нормаль MN в точке А₇ спирали. Касательная в точке А₇ перпендикулярна нормали MN.

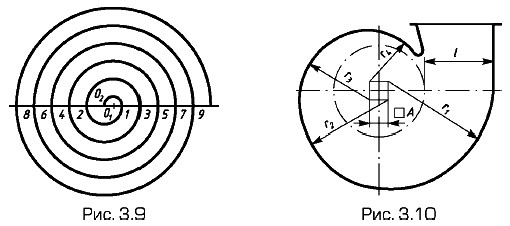
Эвольвенты также относятся к спиралям; они имеют две ветви в зависимости от направления развертывания кривой.

На практике используют и спирали, составленные из дуг окружностей (их называют завитками), проводимых из двух, трех и более центров, расположенных в вершинах правильных многоугольников (на рис. 3.9 из двух центров — О₁ и O₂).

На рис. 3.10 — пример использования четырехцентрового завитка в очертании центробежного вентилятора.

Синусоиду (рис. 3.11) строят по заданному диаметру начальной окружности. Выбирают начало координат, совпадающее с точкой А на окружности заданного радиуса R, и на продолжении оси ОА откладывают отрезок АА₁ = 2πR (равный длине окружности). Делят окружность и отрезок AA₁ на одинаковое число равных частей и пронумеровывают точки деления. Через точки деления окружности проводят ряд прямых, параллельных АА₁; из точек деления прямой АА₁ — ряд прямых, перпендикулярных AA₁. На пересечении этих вспомогательных прямых, имеющих одноименные номера, отмечают точки синусоиды.

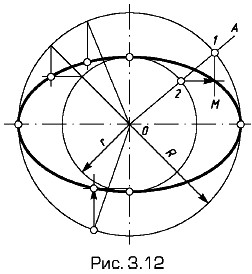
Вид синусоиды имеют многие кривые, изображающие гармонические колебательные процессы или являющиеся проекциями винтовых линий. Для их построения выполнение условия АА₁ = 2πR не является обязательным, но принцип деления исходной окружности и прямой АА₁ сохраняют.

Кривые 2-го порядка. Их свойства — геометрические, баллистические, оптические, акустические и др.— широко используют в самых разнообразных отраслях науки и техники.

Эллипс — множество точек плоскости, сумма расстояний (радиусов-векторов) каждой из которых до двух данных точек той же плоскости (фокусов. От лат. focus — огонь, очаг.) есть величина постоянная (равная 2R — большой оси эллипса).

Один из вариантов построения эллипса по большой (2R) и малой (2r) осям приведен на рис. 3.12. При построении проводят окружности радиусами r и R из одного центра О и произвольный радиус ОА. Из точек пересечения 1 и 2 проводят прямые, параллельные осям эллипса, и в точке их пересечения отмечают точку М эллипса. Аналогично строят необходимое число точек.

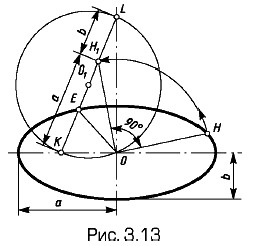
Построение осей эллипса по заданным его сопряженным диаметрам. Поворачивают один из сопряженных полудиаметров на 90° (рис. 3.13). Полученную точку H₁ соединяют с точкой E и из точки O₁ делящей отрезок Н₁Е пополам, проводят дугу радиуса OO_1. Точки L и K определят направлений осей, а их величины — отрезки KH₁ и H₁L. Построение не изменится, если использовать острый угол между сопряженными полудиаметрами.

<<< К началу параграфа                       Окончание параграфа >>>