Главная >> Машиностроительное черчение. Инженерная графика. Чекмарев

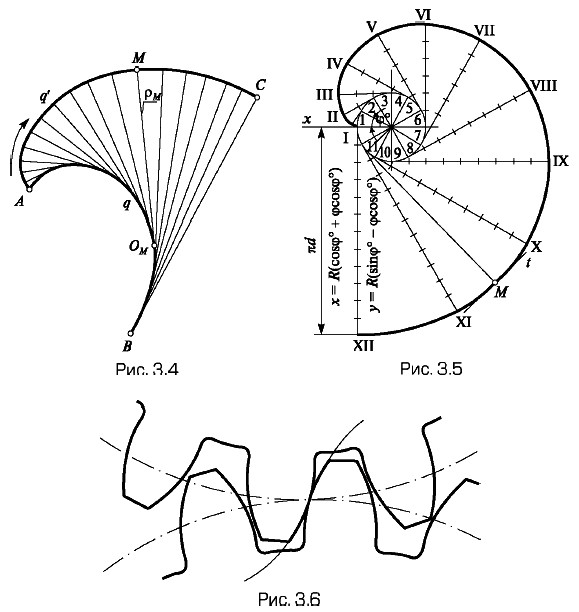
Кривые линии и их применение в чертежах

Плоские кривые линии

Кривую линию называют плоской, если все точки линии лежат в одной плоскости, и пространственной, если точки не принадлежат одной плоскости. Примеры плоских кривых — эвольвента, циклоида, спираль Архимеда, синусоида; кривые второго порядка — эллипс, гипербола, парабола, различные овалы и другие; примеры пространственных кривых — винтовая линия, линия пересечения боковых поверхностей прямых круговых цилиндра и конуса, оси которых не пересекаются. Рассмотрим некоторые из них, применяемые в конструкциях деталей.

Построение эвольвенты

Эвольвентой q' называется кривая, которую описывает точка M прямой ρ_M линии, катящейся без скольжения по неподвижной кривой q (эволюте) AB (рис. 3.4). Центр O_M радиуса кривизны ρ_M точка M. Эвольвента окружности широко (рис. 3.5) применяется в технике для выполнения зубчатых колес (рис. 3.6). Утолщенной линией выделены участки профилей зубьев, выполненных по эвольвенте.

Построение эвольвенты окружности выполняют следующим образом (см. рис. 3.5). Окружность делят на n равных частей, например 12, в точках делений проводят полукасательные и откладывают на последней, 12-й полукасательной отрезок, равный длине окружности. Отрезок делят на п равных частей. На 11-й полукасательной откладывают 11 частей отрезка, на 10-й — 10 и т.д. Через полученные точки проводят с помощью лекала плавную кривую. На рисунке показано построений касательной в произвольной точке M эвольвенты.

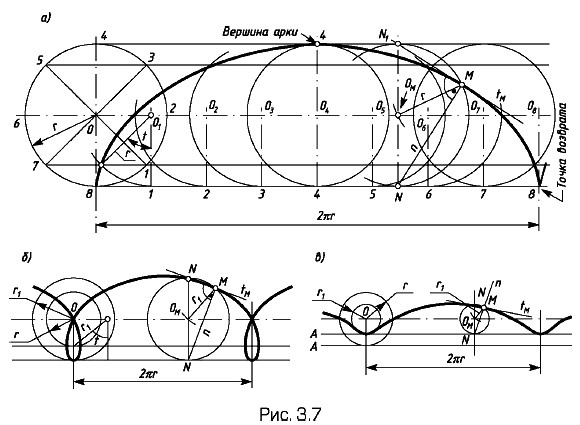
Построение циклических кривых (греч. цикл — колесо, круг). Эти кривые составляют обширный класс кривых, образованных траекториями точек плоскости круга, катящегося без скольжения по какой-либо компланарной с ним направляющей линии. Если эта линия — прямая, траектории точек — обыкновенная циклоида (рис. 3.7, а); укороченная циклоида — точки лежат внутри круга (рис. 3.7, б); удлиненная циклоида — точки лежат вне круга (рис. 3.7, в).

Построение циклоиды: на направляющей прямой откладывают отрезок, равный длине окружности катящегося круга, и делят его на п равных частей (рис 3.7, а). В точках делений восставляют перпендикуляры. На n равных частей делят окружность и через них проводят прямые, параллельные направляющей. Когда круг из положения О переместится в положение О₁ точка 8 поднимется до параллели 7. На этом основании засекают из центра O₁ радиусом, равным радиусу круга, точку на параллели 7, из O₂ засекают точку на параллели 6 и т.д. Через полученные точки проводят плавную кривую.

Построение касательной в произвольной точке M циклоиды: находят положение катящегося круга, когда он проходит через точку М, и проводят через найденный центр O_M диаметр NN₁ Отрезок NM определит полунормаль, a N₁M — полукасательную.

Подобным же образом строят укороченную и удлиненную циклоиды, но параллели проводят через точки деления вспомогательного круга радиусом r₁ = ОМ (см. рис. 3.7, б, в). Этим радиусом и делают засечки из центров O₁, O₂, ... на соответствующих горизонталях.

Продолжение параграфа >>>