|
|
|
|
|
§ 9. Структурное программирование Рекурсивные алгоритмы
Иначе это можно записать так: F(n) = 1 при n ≤ 1; F(n) = F(n - 1) • n при n > 1. В определении факториала через рекурсию имеется условие n ≤ 1, при достижении которого вызов рекурсии прекращается.
S(n) = n при n < 10; S(n) = S(n div 10) + n mod 10 при n ≥ 10.
F(n) = 1 при n ≤ 2; F(n) = F(n - 1) + 3 • F(n - 2) при n > 2. Требуется выяснить, чему равно значение функции F(7). По условию, F(1) = F(2) = 1. F(3) = F(2) + 3 • F(1) =1 + 3 • 1=4.
Подобные вычисления можно проводить в уме, а их результаты фиксировать в таблице:
1) прибавь 1;
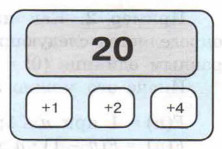
С помощью первой из них исполнитель увеличивает число на экране на 1, с помощью второй — на 2, с помощью третьей — на 4. Программа для исполнителя Плюс — это последовательность команд. Выясним, сколько разных программ, преобразующих число 20 в число 30, можно составить для этого исполнителя. Количество программ, с помощью которых можно получить некоторое число n, будем рассматривать как функцию К(n).
|
|
|



 Алгоритм называется рекурсивным, если на каком-либо шаге он прямо или косвенно обращается сам к себе.
Алгоритм называется рекурсивным, если на каком-либо шаге он прямо или косвенно обращается сам к себе.
 Пример 2. Как известно, факториал натурального числа п определяется следующим образом: n! = 1 • 2 • 3 • ... • n, 0! считается равным единице (0! = 1).
Пример 2. Как известно, факториал натурального числа п определяется следующим образом: n! = 1 • 2 • 3 • ... • n, 0! считается равным единице (0! = 1).
 Самостоятельно определите функцию К(n), которая возвращает количество цифр заданного натурального числа n.
Самостоятельно определите функцию К(n), которая возвращает количество цифр заданного натурального числа n.
 Пример 4. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
Пример 4. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями: